 por Questioner » Sáb Jul 17, 2010 14:54
por Questioner » Sáb Jul 17, 2010 14:54
Olá!
Fiquei na dúvida se postava aqui em G.A. ou em Cálculo... Enfim!
O problema é o seguinte:
Determine a área da região englobada pelo laço interno da limaçon:

[Sugestão: r < ou = 1 sobre o intervalo de integração.]Pois bem. Percebe-se que a limaçon em questão tem um laço visto que 1/b = 1/2 = 0,5.
Da mesma maneira, a está deitada para a esquerda (equação cosseno e positiva).
Pensando na simetria, achei que a equação fica zerada quando:
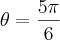
ou
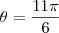
Mas usando os limites de integração
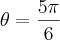
ou

o resultado não bate. De acordo com o solucionário, o limite de integração seria:

e
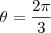
Ele multiplicou a integral por 2, visto que usou simetria.
Alguém pode me explicar estes limites?
Resposta da integral:
![\theta = \pi - \frac{3\sqrt[]{3}}{2} \theta = \pi - \frac{3\sqrt[]{3}}{2}](/latexrender/pictures/6a0c1027fb7adca080d3d1ce0d4c6025.png)
-
Questioner
- Usuário Ativo

-
- Mensagens: 11
- Registrado em: Ter Abr 20, 2010 22:13
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica
- Andamento: cursando
 por Molina » Sáb Jul 17, 2010 15:36
por Molina » Sáb Jul 17, 2010 15:36
Boa tarde, amigo.
Confesso que não conhecia essa região. Na verdade já a vi mas não liguei o nome à imagem. Pesquisando achei alguém com sua mesma dúvida, e já foi resolvido:
yahoo answersGostei dessa animação:


Diego Molina |
CV |
FB |
.COMEquipe AjudaMatemática.com"Existem 10 tipos de pessoas: as que conhecem o sistema binário e as que não conhecem."
-

Molina
- Colaborador Moderador - Professor

-
- Mensagens: 1551
- Registrado em: Dom Jun 01, 2008 14:10
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura em Matemática - UFSC
- Andamento: formado
 por Questioner » Sáb Jul 17, 2010 18:37
por Questioner » Sáb Jul 17, 2010 18:37
Caro Molina,
obrigado pela animação e pelo link. Foram de grande ajuda.
Muito obrigado!
-
Questioner
- Usuário Ativo

-
- Mensagens: 11
- Registrado em: Ter Abr 20, 2010 22:13
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica
- Andamento: cursando
Voltar para Geometria Analítica
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Coordenadas Polares
 por Bruhh » Seg Mar 21, 2011 15:39
por Bruhh » Seg Mar 21, 2011 15:39
- 4 Respostas
- 4039 Exibições
- Última mensagem por Bruhh

Ter Mar 22, 2011 14:22
Cálculo: Limites, Derivadas e Integrais
-
- Coordenadas polares
por suziquim » Seg Mai 16, 2011 17:31
- 2 Respostas
- 1841 Exibições
- Última mensagem por suziquim

Ter Mai 17, 2011 11:15
Cálculo: Limites, Derivadas e Integrais
-
- Coordenadas polares
por manuoliveira » Ter Nov 20, 2012 09:03
- 1 Respostas
- 1794 Exibições
- Última mensagem por MarceloFantini

Ter Nov 20, 2012 09:57
Cálculo: Limites, Derivadas e Integrais
-
- [coordenadas polares]
por FERNANDA_03 » Qui Jul 11, 2013 23:10
- 2 Respostas
- 2706 Exibições
- Última mensagem por FERNANDA_03

Sex Jul 26, 2013 09:58
Cálculo
-
- esboço de coordenadas polares
por Priscila_moraes » Ter Nov 22, 2011 12:52
- 2 Respostas
- 1856 Exibições
- Última mensagem por MarceloFantini

Qua Nov 23, 2011 16:21
Geometria Analítica
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
(FGV) ... função novamente rs
Autor:
my2009 - Qua Dez 08, 2010 21:48
Uma função polinomial f do 1° grau é tal que f(3) = 6 e f(4) = 8.Portanto o valor de f(10) é :
Assunto:
(FGV) ... função novamente rs
Autor: Anonymous - Qui Dez 09, 2010 17:25
Uma função de 1º grau é dada por

.
Temos que para

,

e para

,

.

Ache o valor de

e

, monte a função e substitua

por

.
Assunto:
(FGV) ... função novamente rs
Autor:
Pinho - Qui Dez 16, 2010 13:57
my2009 escreveu:Uma função polinomial f do 1° grau é tal que f(3) = 6 e f(4) = 8.Portanto o valor de f(10) é :
f(x)= 2.x
f(3)=2.3=6
f(4)=2.4=8
f(10)=2.10=20
Assunto:
(FGV) ... função novamente rs
Autor:
dagoth - Sex Dez 17, 2010 11:55
isso ai foi uma questao da FGV?
haahua to precisando trocar de faculdade.
Assunto:
(FGV) ... função novamente rs
Autor:
Thiago 86 - Qua Mar 06, 2013 23:11
Saudações!

ví suaquestão e tentei resolver, depois você conta-me se eu acertei.
Uma função de 1º grau é dada por y=3a+b
Resposta :
3a+b=6 x(4)
4a+b=8 x(-3)
12a+4b=24
-12a-3b=-24
b=0
substituindo b na 1°, ttenho que: 3a+b=6
3a+0=6
a=2
substituindo em: y=3a+b
y=30+0
y=30

Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.

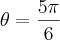 ou
ou 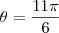
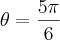 ou
ou  o resultado não bate. De acordo com o solucionário, o limite de integração seria:
o resultado não bate. De acordo com o solucionário, o limite de integração seria: e
e 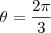
![\theta = \pi - \frac{3\sqrt[]{3}}{2} \theta = \pi - \frac{3\sqrt[]{3}}{2}](/latexrender/pictures/6a0c1027fb7adca080d3d1ce0d4c6025.png)





 .
. ,
,  e para
e para  ,
,  .
.
 e
e  , monte a função e substitua
, monte a função e substitua  por
por  .
.
