Determinar o valor de m para que seja de 30º o ângulo entre os planos
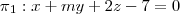
e
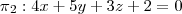
Ok, faço certinho, obtenho os 2 pontos e jogo na fórmula:
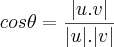
Porém de jeito nenhum chego a resposta, que é segundo o gabarito do livro, 1 ou 7
Alguém poderia ajudar?
Abraços.

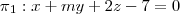
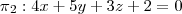
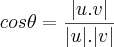


Fantini escreveu:
 ,
,  é sempre não-nulo, assim:
é sempre não-nulo, assim: , temos:
, temos: 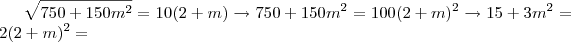
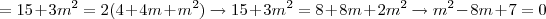 cujas raízes são:
cujas raízes são:  e
e 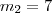 , ambas compreendidas na condição de contorno do intervalo.
, ambas compreendidas na condição de contorno do intervalo.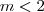 , temos:
, temos: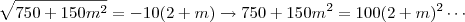 que conduzirá às mesmas raízes do caso anterior, mas estas estarão, agora, fora do intervalo definido.
que conduzirá às mesmas raízes do caso anterior, mas estas estarão, agora, fora do intervalo definido. pode assumir são:
pode assumir são: 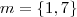


Voltar para Geometria Analítica
Usuários navegando neste fórum: Nenhum usuário registrado e 2 visitantes
![\frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}} \frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}}](/latexrender/pictures/981987c7bcdf9f8f498ca4605785636a.png)
![\sqrt[]{2} \sqrt[]{2}](/latexrender/pictures/f21662d1cabab6e8b273a4b6f1cd663a.png) (dica : igualar a expressão a
(dica : igualar a expressão a  e elevar ao quadrado os dois lados)
e elevar ao quadrado os dois lados)