Olá
marquinhoibvb, boa noite, seja bem-vindo!
Os dois pontos extremos dados da diagonal do losango já permitem que você encontre a reta que os contém. Comentarei as etapas:
O primeiro passo é encontrar o coeficiente angular desta reta, ou seja, sua inclinação.
Sendo a reta não perpendicular ao eixo x (não vertical), ela possuirá uma inclinação de um ângulo

com o eixo x. O "coeficiente angular" é a tangente deste ângulo, calculada através das coordenadas dos dois pontos.
Se chamamos de

este coeficiente angular, assim como
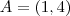
e
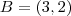
, então:
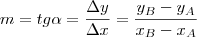
Assim, teremos o coeficiente angular da reta que contém

e

.
Com ele, e escolhendo um dos dois pontos, obtemos a equação da reta, substituindo o ponto escolhido em
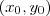
:
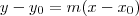
Com a equação desta reta, que podemos chamar de

, e seu o coeficiente angular
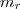
, agora o próximo passo é utilizar a propriedade do losango que possui as diagonais "perpendiculares".
Se as diagonais são perpendiculares, as retas que as contém também são perpendiculares, ou seja, a outra reta

procurada é perpendicular à

, de modo que o produto de seus coeficientes angulares é:
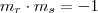
Daqui, encontramos o coeficiente angular da outra reta

(da outra diagonal do losango).
Agora, resta saber um ponto por onde ela passa, utilizando outra propriedade dos paralelogramos (o losango é um paralelogramo):
Suas diagonais se interceptam em seus pontos médios.
Então, encontre as coordenadas do ponto médio do segmento dado, pois a reta

também passará por este ponto.
Com as coordenadas deste ponto médio e o coeficiente angular
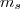
, encontrará a equação procurada:
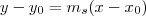
Após este trabalho, bastará localizar a alternativa.
Comente caso tenha alguma dificuldade na resolução.
Tendo dois pontos, você também pode encontrar a equação da reta por determinante. Tópico relacionado:
viewtopic.php?f=117&t=271
Espero ter ajudado!


 com o eixo x. O "coeficiente angular" é a tangente deste ângulo, calculada através das coordenadas dos dois pontos.
com o eixo x. O "coeficiente angular" é a tangente deste ângulo, calculada através das coordenadas dos dois pontos. este coeficiente angular, assim como
este coeficiente angular, assim como 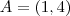 e
e 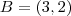 , então:
, então: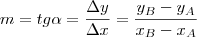
 e
e  .
.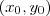 :
: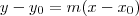
 , e seu o coeficiente angular
, e seu o coeficiente angular 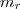 , agora o próximo passo é utilizar a propriedade do losango que possui as diagonais "perpendiculares".
, agora o próximo passo é utilizar a propriedade do losango que possui as diagonais "perpendiculares". procurada é perpendicular à
procurada é perpendicular à 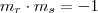
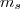 , encontrará a equação procurada:
, encontrará a equação procurada: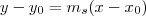



 substitui-se
substitui-se 
 não existem zeros.Senão vejamos
não existem zeros.Senão vejamos

 .Como se pode observar o vertice está acima do eixo Ox, estando parabola virada para cima, o vertice é um mínimo absoluto.Então basta calcular a função para os valores dos extremos do intervalo.
.Como se pode observar o vertice está acima do eixo Ox, estando parabola virada para cima, o vertice é um mínimo absoluto.Então basta calcular a função para os valores dos extremos do intervalo.