Oii gente, primeira vez no fórum então me desculpem qualquer coisa, a questão é a seguinte:
Encontre um vetor unitário que seja ortogonal ao plano que passa pelos pontos A(1,1,0), B(1,0,1) e C(0,1,1).
O problema é que eu não sei nem por onde começar, eu sei fazer um vetor ortogonal que passa por esses pontos, mas eu não sei o que seria um "vetor unitário" e o que isso muda na resolução, se alguém puder me ajudar eu ficaria grata.
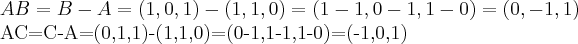
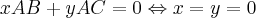
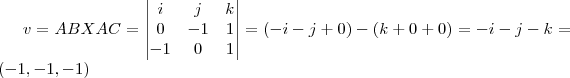
![{u}_{v}=(v/\left|v \right|)
\left|v \right|=\sqrt[]{(-1)^2+(-1)^2+(-1)^2}=\sqrt[]{3}
{u}_{v}=(-1/\sqrt[]{3},-1/\sqrt[]{3},-1/\sqrt[]{3})](/latexrender/pictures/8a0b1982884a18a22a9b88a180f1d008.png "{u}_{v}=(v/\left|v \right|)
\left|v \right|=\sqrt[]{(-1)^2+(-1)^2+(-1)^2}=\sqrt[]{3}
{u}_{v}=(-1/\sqrt[]{3},-1/\sqrt[]{3},-1/\sqrt[]{3})")
![\frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}}](/latexrender/pictures/981987c7bcdf9f8f498ca4605785636a.png "\frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}}")
![\sqrt[]{2}](/latexrender/pictures/f21662d1cabab6e8b273a4b6f1cd663a.png "\sqrt[]{2}")
e elevar ao quadrado os dois lados)