 por GFerraz » Seg Abr 24, 2017 20:37
por GFerraz » Seg Abr 24, 2017 20:37
Esse exercício é do livro do Nathan Moreira dos Santos, "Vetores e Matrizes".
Mostre que as retas
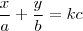
,
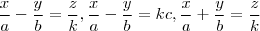
, para
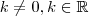
estão inteiramente contidas no paraboloide hiperbólico
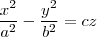
Meu problema é: Não vejo um modo de demonstrar que isso é válido

Gostaria de alguma sugestão de como fazer isso, pois não vejo saída disso.
-
GFerraz
- Novo Usuário

-
- Mensagens: 3
- Registrado em: Seg Abr 24, 2017 19:58
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Bacharelado em Engenharia Mecânica
- Andamento: cursando
Voltar para Geometria Analítica
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [QUÁDRICAS] parabolóide hiperbólico, parábolas...
por Sohrab » Ter Abr 16, 2013 20:24
- 2 Respostas
- 1961 Exibições
- Última mensagem por young_jedi

Qua Abr 17, 2013 11:39
Geometria Analítica
-
- [2º Axioma de Ordem] não prova infinitos pontos em reta
 por Luiz Augusto Prado » Sex Mar 09, 2012 01:15
por Luiz Augusto Prado » Sex Mar 09, 2012 01:15
- 1 Respostas
- 2330 Exibições
- Última mensagem por Luiz Augusto Prado

Sáb Mar 10, 2012 01:20
Geometria Plana
-
- Paraboloide
por Man Utd » Qua Jul 31, 2013 16:30
- 2 Respostas
- 4688 Exibições
- Última mensagem por Man Utd

Qui Ago 01, 2013 19:12
Geometria Analítica
-
- paraboloide
 por gvt123 » Qui Jun 18, 2020 18:12
por gvt123 » Qui Jun 18, 2020 18:12
- 0 Respostas
- 1942 Exibições
- Última mensagem por gvt123

Qui Jun 18, 2020 18:12
Geometria Analítica
-
- Calculo dos angulos internos dum triangulo hiperbólico
por Jhenrique » Ter Jul 24, 2012 18:42
- 0 Respostas
- 1817 Exibições
- Última mensagem por Jhenrique

Ter Jul 24, 2012 18:42
Geometria Espacial
Usuários navegando neste fórum: Nenhum usuário registrado e 3 visitantes
Assunto:
[Função] do primeiro grau e quadratica
Autor:
Thassya - Sáb Out 01, 2011 16:20
1) Para que os pontos (1,3) e (-3,1) pertençam ao grafico da função f(X)=ax + b ,o valor de b-a deve ser ?
2)Qual o maior valor assumido pela função f : [-7 ,10] em R definida por f(x) = x ao quadrado - 5x + 9?
3) A função f, do primeiro grau, é definida pos f(x)= 3x + k para que o gráfico de f corte o eixo das ordenadas no ponto de ordenada 5 é?
Assunto:
[Função] do primeiro grau e quadratica
Autor:
Neperiano - Sáb Out 01, 2011 19:46
Ola
Qual as suas dúvidas?
O que você não está conseguindo fazer?
Nos mostre para podermos ajudar
Atenciosamente
Assunto:
[Função] do primeiro grau e quadratica
Autor:
joaofonseca - Sáb Out 01, 2011 20:15
1)Dados dois pontos A=(1,3) e B=(-3,1) de uma reta, é possivel definir a sua equação.


Em

substitui-se
m, substitui-se
y e
x por um dos pares ordenados, e resolve-se em ordem a
b.

2)Na equação

não existem zeros.Senão vejamos
Completando o quadrado,

As coordenadas do vertice da parabola são

O eixo de simetria é a reta

.Como se pode observar o vertice está acima do eixo Ox, estando parabola virada para cima, o vertice é um mínimo absoluto.Então basta calcular a função para os valores dos extremos do intervalo.
f(-7)=93
f(10)=59
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
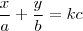 ,
, 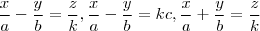 , para
, para 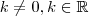 estão inteiramente contidas no paraboloide hiperbólico
estão inteiramente contidas no paraboloide hiperbólico 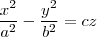
 Gostaria de alguma sugestão de como fazer isso, pois não vejo saída disso.
Gostaria de alguma sugestão de como fazer isso, pois não vejo saída disso.
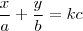 ,
, 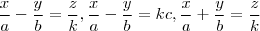 , para
, para 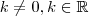 estão inteiramente contidas no paraboloide hiperbólico
estão inteiramente contidas no paraboloide hiperbólico 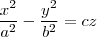
 Gostaria de alguma sugestão de como fazer isso, pois não vejo saída disso.
Gostaria de alguma sugestão de como fazer isso, pois não vejo saída disso.


 substitui-se m, substitui-se y e x por um dos pares ordenados, e resolve-se em ordem a b.
substitui-se m, substitui-se y e x por um dos pares ordenados, e resolve-se em ordem a b.
 não existem zeros.Senão vejamos
não existem zeros.Senão vejamos

 .Como se pode observar o vertice está acima do eixo Ox, estando parabola virada para cima, o vertice é um mínimo absoluto.Então basta calcular a função para os valores dos extremos do intervalo.
.Como se pode observar o vertice está acima do eixo Ox, estando parabola virada para cima, o vertice é um mínimo absoluto.Então basta calcular a função para os valores dos extremos do intervalo.