 por lucassouza » Sáb Abr 11, 2015 02:17
por lucassouza » Sáb Abr 11, 2015 02:17
Olá estou com dificuldades, a questão pede:
determinar as equações vetoriais, paramétricas, simetricas e reduzidas...
na alternativa "d" pede para achar a equação "possui o ponto M (1,5,–2) e é paralela à reta determinada pelos pontos
A(5,–2,3) e B(–1,–4,3)"
só que não estou conseguindo entender como vou achar o vetor diretor, entende?
a resposta da equação vetorial é P=(1,5,–2) +m(3,1,0)
-
lucassouza
- Usuário Dedicado

-
- Mensagens: 29
- Registrado em: Seg Set 15, 2014 15:03
- Formação Escolar: SUPLETIVO
- Andamento: cursando
 por DanielFerreira » Sáb Abr 11, 2015 09:08
por DanielFerreira » Sáb Abr 11, 2015 09:08
Lucas, bom dia!
Encontre o
vetor diretor da reta que passa pelos pontos A e B; esse vetor deverá ser proporcional ao vetor diretor da reta a ser encontrada, pois são paralelos.
Considere
r sendo a reta que passa por A e B, então:
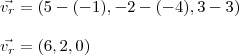
Ora, de acordo com o que foi exposto acima (paralelismo), temos que
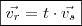
; onde
s é a rqueeta a ser encontrada.
Desde que
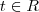
, poderás atribuir qualquer valor a ele. De acordo com o gabarito apresentado, escolheu-se

!
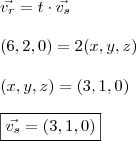
Logo,
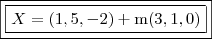
"Sabedoria é saber o que fazer;
habilidade é saber como fazer;
virtude é fazer."
(David S. Jordan)
--------------------------------------------------------------------------------
-
DanielFerreira
- Colaborador - em formação

-
- Mensagens: 1732
- Registrado em: Qui Jul 23, 2009 21:34
- Localização: Mangaratiba - RJ
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura em Matemática - IFRJ
- Andamento: formado
-
 por lucassouza » Sáb Abr 11, 2015 10:17
por lucassouza » Sáb Abr 11, 2015 10:17
Velho, grato desde já, se eu responder desta maneira como está na imagem estaria correto? é porque quando fala em passar pelos pontos AB vem logo à minha cabeça segmento de reta, e para achar o vetor faço B-A... Só que o vetor fica negativo, na sua resolução ficou (6,2,0) como fiz ficou (-6,-2,0). Tbm pertence aos reais oO.
- Anexos
-

-
lucassouza
- Usuário Dedicado

-
- Mensagens: 29
- Registrado em: Seg Set 15, 2014 15:03
- Formação Escolar: SUPLETIVO
- Andamento: cursando
 por DanielFerreira » Sáb Abr 11, 2015 16:56
por DanielFerreira » Sáb Abr 11, 2015 16:56
Lucas, tua resolução também está correta! Afim de obter o vetor diretor da reta positivo poderia ter multiplicado por
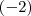
, em vez de

. O importante é haver proporcionalidade entre eles!!
"Sabedoria é saber o que fazer;
habilidade é saber como fazer;
virtude é fazer."
(David S. Jordan)
--------------------------------------------------------------------------------
-
DanielFerreira
- Colaborador - em formação

-
- Mensagens: 1732
- Registrado em: Qui Jul 23, 2009 21:34
- Localização: Mangaratiba - RJ
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura em Matemática - IFRJ
- Andamento: formado
-
Voltar para Geometria Analítica
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [Equação da Reta] Reta que passa por pontos do plano.
por acorreia » Qua Mai 02, 2012 17:31
- 1 Respostas
- 2469 Exibições
- Última mensagem por Russman

Qua Mai 02, 2012 21:25
Geometria Analítica
-
- [Estudo da reta] Determinar a equação de uma reta
por Isabelagarcia » Qui Jul 24, 2014 23:45
- 0 Respostas
- 1599 Exibições
- Última mensagem por Isabelagarcia

Qui Jul 24, 2014 23:45
Geometria Analítica
-
- [Equação da reta] Encontrando equação paramétrica.
por Vitor Sanches » Qua Jun 26, 2013 17:54
- 0 Respostas
- 6098 Exibições
- Última mensagem por Vitor Sanches

Qua Jun 26, 2013 17:54
Geometria Analítica
-
- Equação da Reta
por aline2010 » Dom Jun 13, 2010 23:16
- 1 Respostas
- 1658 Exibições
- Última mensagem por Elcioschin

Seg Jun 14, 2010 12:16
Geometria Analítica
-
- Equação da reta
por marcio277 » Sex Nov 19, 2010 15:04
- 1 Respostas
- 1528 Exibições
- Última mensagem por Molina

Sex Nov 19, 2010 15:13
Geometria Plana
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
simplifiquei e achei...está certo?????????????
Autor:
zig - Sex Set 23, 2011 13:57
![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]} {(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]}](/latexrender/pictures/19807748a214d3361336324f3e43ea9a.png)
![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}} {(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}}](/latexrender/pictures/3d7908e5b4e397bf635b6546063d9130.png)
Assunto:
simplifiquei e achei...está certo?????????????
Autor:
Vennom - Sex Set 23, 2011 21:41
zig escreveu:![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]} {(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]}](/latexrender/pictures/19807748a214d3361336324f3e43ea9a.png)
![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}} {(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}}](/latexrender/pictures/3d7908e5b4e397bf635b6546063d9130.png)
Rpz, o negócio é o seguinte:
Quando você tem uma potência negativa, tu deve inverter a base dela. Por exemplo:

Então pense o seguinte: a fração geratriz de 0,05 é

, ou seja, 1 dividido por 20 é igual a 0.05 . Sendo assim, a função final é igual a vinte elevado à meio.
Veja:
![{0,05}^{-\frac{1}{2}} = {\frac{1}{20}}^{-\frac{1}{2}} = {\frac{20}{1}}^{\frac{1}{2}} = \sqrt[2]{20} {0,05}^{-\frac{1}{2}} = {\frac{1}{20}}^{-\frac{1}{2}} = {\frac{20}{1}}^{\frac{1}{2}} = \sqrt[2]{20}](/latexrender/pictures/c0100c6f4d8bdbb7d54165e6be7aff04.png)
A raiz quadrada de vinte, você acha fácil, né?
Espero ter ajudado.
Assunto:
simplifiquei e achei...está certo?????????????
Autor:
fraol - Dom Dez 11, 2011 20:23
Nós podemos simplificar, um pouco,

da seguinte forma:

.
É isso.
Assunto:
simplifiquei e achei...está certo?????????????
Autor:
fraol - Dom Dez 11, 2011 20:24
Nós podemos simplificar, um pouco,

da seguinte forma:

.
É isso.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.


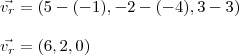
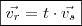 ; onde
; onde 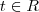 , poderás atribuir qualquer valor a ele. De acordo com o gabarito apresentado, escolheu-se
, poderás atribuir qualquer valor a ele. De acordo com o gabarito apresentado, escolheu-se  !
!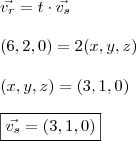
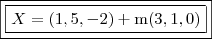

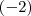 , em vez de
, em vez de  . O importante é haver proporcionalidade entre eles!!
. O importante é haver proporcionalidade entre eles!!![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]} {(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]}](/latexrender/pictures/19807748a214d3361336324f3e43ea9a.png)
![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}} {(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}}](/latexrender/pictures/3d7908e5b4e397bf635b6546063d9130.png)

 , ou seja, 1 dividido por 20 é igual a 0.05 . Sendo assim, a função final é igual a vinte elevado à meio.
, ou seja, 1 dividido por 20 é igual a 0.05 . Sendo assim, a função final é igual a vinte elevado à meio. ![{0,05}^{-\frac{1}{2}} = {\frac{1}{20}}^{-\frac{1}{2}} = {\frac{20}{1}}^{\frac{1}{2}} = \sqrt[2]{20} {0,05}^{-\frac{1}{2}} = {\frac{1}{20}}^{-\frac{1}{2}} = {\frac{20}{1}}^{\frac{1}{2}} = \sqrt[2]{20}](/latexrender/pictures/c0100c6f4d8bdbb7d54165e6be7aff04.png)
 da seguinte forma:
da seguinte forma: .
. da seguinte forma:
da seguinte forma: .
.