 por Pessoa Estranha » Qua Jan 01, 2014 01:27
por Pessoa Estranha » Qua Jan 01, 2014 01:27
MOSTRAR QUE A AMPLITUDE DA ELIPSE É DADA POR
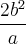
.
Minha resolução:
Consideremos PQ o segmento cuja medida é a amplitude da elipse. Conforme a definição da mesma e o Teorema de Pitágoras, considerando F1 e F2 os focos, temos:
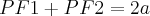
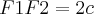
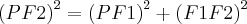
Então:
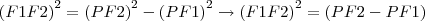
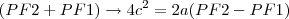
---->
---->
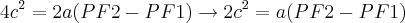
Porém, pela definição, vem que:
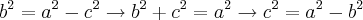
E, aplicando no resultado, temos:

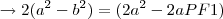

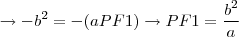
Já tentei resolver outras vezes, mas sempre cheguei no mesmo resultado. Qual é o erro? Por favor, ajudem!
Obrigada!
-
Pessoa Estranha
- Colaborador Voluntário

-
- Mensagens: 262
- Registrado em: Ter Jul 16, 2013 16:43
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Matemática
- Andamento: cursando
 por Renato_RJ » Qua Jan 01, 2014 09:37
por Renato_RJ » Qua Jan 01, 2014 09:37
Bom dia !!!
Você deseja provar a amplitude da elipse, também conhecida como latus rectum. Mas você somente calculou o semi latus rectum, isto é, apenas a metade, logo basta multiplicar o seu resultado por 2.
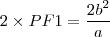
Abraços,
Renato.
Iniciando a minha "caminhada" pela matemática agora... Tenho muito o quê aprender...
-

Renato_RJ
- Colaborador Voluntário

-
- Mensagens: 306
- Registrado em: Qui Jan 06, 2011 15:47
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Mestrado em Matemática
- Andamento: cursando
 por Pessoa Estranha » Qua Jan 01, 2014 11:15
por Pessoa Estranha » Qua Jan 01, 2014 11:15
Bom dia! Feliz Ano Novo!
Obrigada por responder!
Agora eu entendi. Achava que a amplitude da elipse era só o tamanho do segmento perpendicular ao eixo focal e cujas extremidades eram um dos focos e um ponto pertencente à elipse. Estranho.... Acabei fixando a ideia e, agora, ficou esquisito....
Obrigada!

-
Pessoa Estranha
- Colaborador Voluntário

-
- Mensagens: 262
- Registrado em: Ter Jul 16, 2013 16:43
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Matemática
- Andamento: cursando
 por Renato_RJ » Qua Jan 01, 2014 15:15
por Renato_RJ » Qua Jan 01, 2014 15:15
Pessoa Estranha escreveu:Bom dia! Feliz Ano Novo!
Obrigada por responder!
Agora eu entendi. Achava que a amplitude da elipse era só o tamanho do segmento perpendicular ao eixo focal e cujas extremidades eram um dos focos e um ponto pertencente à elipse. Estranho.... Acabei fixando a ideia e, agora, ficou esquisito....
Obrigada!

Obrigado e um feliz ano novo para você também !!
[ ]'s
Renato.
Iniciando a minha "caminhada" pela matemática agora... Tenho muito o quê aprender...
-

Renato_RJ
- Colaborador Voluntário

-
- Mensagens: 306
- Registrado em: Qui Jan 06, 2011 15:47
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Mestrado em Matemática
- Andamento: cursando
Voltar para Geometria Analítica
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [Geometria Analítica] Elipse
por Pessoa Estranha » Seg Dez 30, 2013 09:37
- 0 Respostas
- 1121 Exibições
- Última mensagem por Pessoa Estranha

Seg Dez 30, 2013 09:37
Geometria Analítica
-
- [Geometria Analítica] Elipse
por Pessoa Estranha » Qui Jan 02, 2014 18:32
- 2 Respostas
- 2037 Exibições
- Última mensagem por Pessoa Estranha

Qui Jan 02, 2014 23:32
Geometria Analítica
-
- [Geometria Analítica] Elipse
por Pessoa Estranha » Qui Jan 02, 2014 18:39
- 0 Respostas
- 1120 Exibições
- Última mensagem por Pessoa Estranha

Qui Jan 02, 2014 18:39
Geometria Analítica
-
- [Desafio] Geometria Analítica - Elipse
por Pessoa Estranha » Qui Jan 02, 2014 18:43
- 1 Respostas
- 5580 Exibições
- Última mensagem por teabiofeul

Seg Out 05, 2015 08:42
Desafios Enviados
-
- [Desafio] Geometria Analítica - Elipse
por Pessoa Estranha » Qui Jan 02, 2014 18:47
- 0 Respostas
- 4207 Exibições
- Última mensagem por Pessoa Estranha

Qui Jan 02, 2014 18:47
Desafios Enviados
Usuários navegando neste fórum: Nenhum usuário registrado e 2 visitantes
Assunto:
(FGV) ... função novamente rs
Autor:
my2009 - Qua Dez 08, 2010 21:48
Uma função polinomial f do 1° grau é tal que f(3) = 6 e f(4) = 8.Portanto o valor de f(10) é :
Assunto:
(FGV) ... função novamente rs
Autor: Anonymous - Qui Dez 09, 2010 17:25
Uma função de 1º grau é dada por

.
Temos que para

,

e para

,

.

Ache o valor de

e

, monte a função e substitua

por

.
Assunto:
(FGV) ... função novamente rs
Autor:
Pinho - Qui Dez 16, 2010 13:57
my2009 escreveu:Uma função polinomial f do 1° grau é tal que f(3) = 6 e f(4) = 8.Portanto o valor de f(10) é :
f(x)= 2.x
f(3)=2.3=6
f(4)=2.4=8
f(10)=2.10=20
Assunto:
(FGV) ... função novamente rs
Autor:
dagoth - Sex Dez 17, 2010 11:55
isso ai foi uma questao da FGV?
haahua to precisando trocar de faculdade.
Assunto:
(FGV) ... função novamente rs
Autor:
Thiago 86 - Qua Mar 06, 2013 23:11
Saudações!

ví suaquestão e tentei resolver, depois você conta-me se eu acertei.
Uma função de 1º grau é dada por y=3a+b
Resposta :
3a+b=6 x(4)
4a+b=8 x(-3)
12a+4b=24
-12a-3b=-24
b=0
substituindo b na 1°, ttenho que: 3a+b=6
3a+0=6
a=2
substituindo em: y=3a+b
y=30+0
y=30

Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
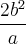 .
.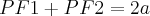
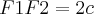
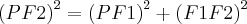
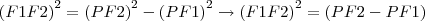
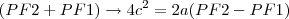 ---->
---->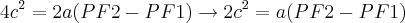
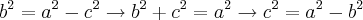

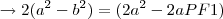

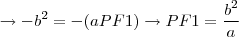


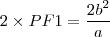

 .
. ,
,  e para
e para  ,
,  .
.
 e
e  , monte a função e substitua
, monte a função e substitua  por
por  .
.