 por Ronaldobb » Seg Dez 02, 2013 23:19
por Ronaldobb » Seg Dez 02, 2013 23:19
Por favor, poderiam me ajudar nessas questões?
1) Determine o simétrico do ponto P(3,1-2) em relação ao ponto A(-1,0,-3).
2) Mostrar que os pontos A(4,0,1), B(5,1,3), C(3,2,5) e D(2,1,3) são vértices de um paralelogramo.
-
Ronaldobb
- Usuário Parceiro

-
- Mensagens: 59
- Registrado em: Ter Set 18, 2012 19:35
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Administração
- Andamento: cursando
 por e8group » Qua Dez 04, 2013 18:01
por e8group » Qua Dez 04, 2013 18:01
Sejam os pontos
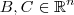
. Considere o segmento de reta
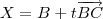
com
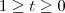
. O ponto

é simétrico de

em relação ao ponto médio do segmento de reta acima (e vice-versa ) . Para exemplificar , com n = 4 . Seja
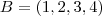
e
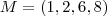
o ponto médio do segmento de reta
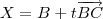
, vamos determinar o ponto

.
Solução :
Suponhamos que
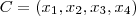
(x_i's a ser determinados ) . Substituindo
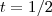
em
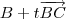
e igualando-o ao ponto
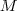
obterá os x_i's .
Tente fazer o item empregando (1) este raciocínio .
2) Tente mostrar que os lados opostos são paralelos e são iguais .
-
e8group
- Colaborador Voluntário

-
- Mensagens: 1400
- Registrado em: Sex Jun 01, 2012 12:10
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica
- Andamento: cursando
Voltar para Geometria Analítica
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [Geometria Analítica] Vetores No Espaço
por felipe10 » Seg Mai 07, 2012 13:16
- 1 Respostas
- 5296 Exibições
- Última mensagem por LuizAquino

Seg Mai 07, 2012 18:55
Geometria Analítica
-
- [pontos/área] Geometria Analítica
por Isaa » Qua Set 10, 2008 18:18
- 2 Respostas
- 4184 Exibições
- Última mensagem por Isaa

Qui Set 11, 2008 13:05
Geometria Analítica
-
- Geometria Analítica : condição de alinhamento de pontos.
 por Larice Mourao » Qui Mai 17, 2012 15:44
por Larice Mourao » Qui Mai 17, 2012 15:44
- 5 Respostas
- 4847 Exibições
- Última mensagem por Larice Mourao

Ter Mai 22, 2012 23:49
Geometria Analítica
-
- [Geometria Analítica] distância entre pontos
por aprendiz007 » Sex Dez 02, 2016 17:58
- 0 Respostas
- 2615 Exibições
- Última mensagem por aprendiz007

Sex Dez 02, 2016 17:58
Geometria Analítica
-
- [Geometria Analítica] Área formada por pontos no plano
por acorreia » Ter Mai 08, 2012 18:05
- 1 Respostas
- 1794 Exibições
- Última mensagem por LuizAquino

Ter Mai 08, 2012 20:36
Geometria Analítica
Usuários navegando neste fórum: Nenhum usuário registrado e 3 visitantes
Assunto:
função demanda
Autor:
ssousa3 - Dom Abr 03, 2011 20:55
alguém poderia me ajudar nesse exercício aqui Uma loja de CDs adquire cada unidade por R$20,00 e a revende por R$30,00. Nestas condições,
a quantidade mensal que consegue vender é 500 unidades. O proprietário estima que, reduzindo o preço para R$28,00, conseguirá vender 600 unidades por mês.
a) Obtenha a função demanda, supondo ser linear
Eu faço ensino médio mas compro apostilas de concursos para me preparar para mercado de trabalho e estudar sozinho não é fácil. Se alguém puder me ajudar aqui fico grato
Assunto:
função demanda
Autor:
ssousa3 - Seg Abr 04, 2011 14:30
Gente alguém por favor me ensine a calcular a fórmula da função demanda

Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.



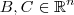 . Considere o segmento de reta
. Considere o segmento de reta 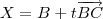 com
com 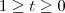 . O ponto
. O ponto  é simétrico de
é simétrico de  em relação ao ponto médio do segmento de reta acima (e vice-versa ) . Para exemplificar , com n = 4 . Seja
em relação ao ponto médio do segmento de reta acima (e vice-versa ) . Para exemplificar , com n = 4 . Seja 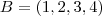 e
e 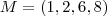 o ponto médio do segmento de reta
o ponto médio do segmento de reta 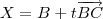 , vamos determinar o ponto
, vamos determinar o ponto  .
. 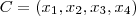 (x_i's a ser determinados ) . Substituindo
(x_i's a ser determinados ) . Substituindo 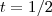 em
em 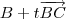 e igualando-o ao ponto
e igualando-o ao ponto 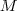 obterá os x_i's .
obterá os x_i's . 
