 por GABRIELA » Ter Set 29, 2009 16:22
por GABRIELA » Ter Set 29, 2009 16:22
calcular a distancia entre os pontos R (5,1) e S (7,9):
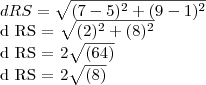
Só que não sei onde estou errando...Podem me mostrar o erRo?
-
GABRIELA
- Usuário Parceiro

-
- Mensagens: 73
- Registrado em: Seg Ago 31, 2009 17:31
- Formação Escolar: ENSINO MÉDIO
- Andamento: cursando
 por Molina » Qua Set 30, 2009 00:56
por Molina » Qua Set 30, 2009 00:56
Boa noite, Gabriela.
O erro está desta linha:
GABRIELA escreveu: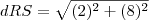
para esta:
GABRIELA escreveu: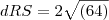
Você só pode "tirar" da raiz, quando tiver uma multiplicação.
Então primeiramente faça a soma dos números que está dentro da raiz e depois fatore, ok?
Bom estudo,

Diego Molina |
CV |
FB |
.COMEquipe AjudaMatemática.com"Existem 10 tipos de pessoas: as que conhecem o sistema binário e as que não conhecem."
-

Molina
- Colaborador Moderador - Professor

-
- Mensagens: 1551
- Registrado em: Dom Jun 01, 2008 14:10
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura em Matemática - UFSC
- Andamento: formado
 por Cleyson007 » Qua Set 30, 2009 18:40
por Cleyson007 » Qua Set 30, 2009 18:40
Boa tarde!
Fómula da distância entre os pontos:
^{2}+{(y}_{2}-{y}_{1})^2 d(R,S)=\sqrt[2]({{{x}_{2}-{x}_{1}})^{2}+{(y}_{2}-{y}_{1})^2](/latexrender/pictures/5ed2774c15f8358559f4e0cec448e958.png)
Quanto à resolução:
^{2}+({9-1})^{2}} d(R,S)=\sqrt[2]({7-5})^{2}+({9-1})^{2}}](/latexrender/pictures/19005fc2578c346ea766c687baea1ad1.png)
![d(R,S)=\sqrt[2]{4+64} d(R,S)=\sqrt[2]{4+64}](/latexrender/pictures/205e0d6b783e43d0129c6f9577bed300.png)
![d(R,S)=\sqrt[2]{68} d(R,S)=\sqrt[2]{68}](/latexrender/pictures/b5950d041ec6ec4090b0c4f1ec9965c0.png)
Gabriela, ao chegar aqui, você deve fatorar o
68![d(R,S)=\sqrt[2]{{2}^{2}.17} d(R,S)=\sqrt[2]{{2}^{2}.17}](/latexrender/pictures/3034de80fda537197b395efe2ffecbb0.png)
Logo,
![d(R,S)=2\sqrt[2]{17} d(R,S)=2\sqrt[2]{17}](/latexrender/pictures/44772b546cfff12d5bc960cac19f8816.png)
Espero que tenha entendido!
Até mais.
Bons estudos!
-

Cleyson007
- Colaborador Voluntário

-
- Mensagens: 1228
- Registrado em: Qua Abr 30, 2008 00:08
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Matemática UFJF
- Andamento: formado
 por GABRIELA » Qua Set 30, 2009 20:44
por GABRIELA » Qua Set 30, 2009 20:44
ahhh entendi! Eu parei no 17 e fiquei sem saber o que fazia.hahuaha

-
GABRIELA
- Usuário Parceiro

-
- Mensagens: 73
- Registrado em: Seg Ago 31, 2009 17:31
- Formação Escolar: ENSINO MÉDIO
- Andamento: cursando
Voltar para Geometria Analítica
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Ajud na questão
por GABRIELA » Ter Set 29, 2009 16:22
- 1 Respostas
- 732 Exibições
- Última mensagem por Cleyson007

Dom Nov 01, 2009 12:38
Geometria Analítica
-
- [Questão POSCOMP 2011] Ajuda para interpretar questão
por hlustosa » Dom Jul 29, 2012 14:54
- 3 Respostas
- 12994 Exibições
- Última mensagem por hlustosa

Seg Jul 30, 2012 01:13
Funções
-
- Questão de P.A.
por mushthielv » Seg Ago 17, 2009 12:21
- 2 Respostas
- 10976 Exibições
- Última mensagem por Elcioschin

Ter Ago 18, 2009 08:54
Progressões
-
- QUESTÃO
por GABRIELA » Ter Set 08, 2009 16:32
- 2 Respostas
- 15120 Exibições
- Última mensagem por GABRIELA

Ter Set 08, 2009 21:21
Matrizes e Determinantes
-
- Questão da FCC
por wanderlymarques » Qua Nov 18, 2009 12:44
- 2 Respostas
- 5034 Exibições
- Última mensagem por wanderlymarques

Qui Nov 19, 2009 12:58
Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
Exercicios de polinomios
Autor:
shaft - Qua Jun 30, 2010 17:30

Então, o exercicio pede para encontrar

.
Bom, tentei resolver a questão acima desenvolvendo as duas partes em ( )...Logo dps cheguei em um resultado q nao soube o q fazer mais.
Se vcs puderem ajudar !
Assunto:
Exercicios de polinomios
Autor:
Douglasm - Qua Jun 30, 2010 17:53
Bom, se desenvolvermos isso, encontramos:

Para que os polinômios sejam iguais, seus respectivos coeficientes devem ser iguais (ax = bx ; ax² = bx², etc.):


Somando a primeira e a segunda equação:

Finalmente:

Até a próxima.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
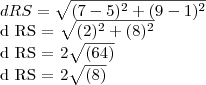

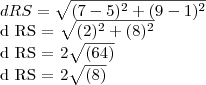



^{2}+{(y}_{2}-{y}_{1})^2 d(R,S)=\sqrt[2]({{{x}_{2}-{x}_{1}})^{2}+{(y}_{2}-{y}_{1})^2](/latexrender/pictures/5ed2774c15f8358559f4e0cec448e958.png)
^{2}+({9-1})^{2}} d(R,S)=\sqrt[2]({7-5})^{2}+({9-1})^{2}}](/latexrender/pictures/19005fc2578c346ea766c687baea1ad1.png)
![d(R,S)=\sqrt[2]{4+64} d(R,S)=\sqrt[2]{4+64}](/latexrender/pictures/205e0d6b783e43d0129c6f9577bed300.png)
![d(R,S)=\sqrt[2]{68} d(R,S)=\sqrt[2]{68}](/latexrender/pictures/b5950d041ec6ec4090b0c4f1ec9965c0.png)
![d(R,S)=\sqrt[2]{{2}^{2}.17} d(R,S)=\sqrt[2]{{2}^{2}.17}](/latexrender/pictures/3034de80fda537197b395efe2ffecbb0.png)
![d(R,S)=2\sqrt[2]{17} d(R,S)=2\sqrt[2]{17}](/latexrender/pictures/44772b546cfff12d5bc960cac19f8816.png)




 .
.



