 por Jhenrique » Seg Dez 10, 2012 18:51
por Jhenrique » Seg Dez 10, 2012 18:51
Olá!
Vendo as vídeo-aulas do Luiz Aquino, especificamente esta: [http://www.youtube.com/watch?v=39f98A-rtsU]
[34. Geometria Analítica - Equação Geral das Cônicas]
Ele demonstra a equação da parábola como:
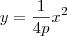
E a quação geral das cônicas como:

Ok! ...
... Mas estamos carecas de saber que a equação da parábola é
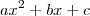
, portanto, a equação da parábola estudada em geometria analítica não é deficiente?
E outra, eu vi um livro que traz a equação geral das cônicas como
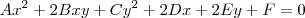
, certamente fazendo alusão ao produto notável:
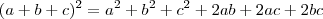
.
E então, que me dizem? Gostaria de
esclarecimentos!Obg!
"A solução errada para o problema certo é anos-luz melhor do que a solução certa para o problema errado." - Russell Ackoff
-
Jhenrique
- Colaborador Voluntário

-
- Mensagens: 180
- Registrado em: Dom Mai 15, 2011 22:37
- Formação Escolar: ENSINO MÉDIO
- Área/Curso: Técnico em Mecânica
- Andamento: formado
 por LuizAquino » Ter Dez 11, 2012 09:25
por LuizAquino » Ter Dez 11, 2012 09:25
Jhenrique escreveu:Olá!
Vendo as vídeo-aulas do Luiz Aquino, especificamente esta: [http://www.youtube.com/watch?v=39f98A-rtsU]
[34. Geometria Analítica - Equação Geral das Cônicas]
Ele demonstra a equação da parábola como:
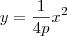
E a quação geral das cônicas como:

Ok! ...
... Mas estamos carecas de saber que a equação da parábola é
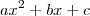
, portanto, a equação da parábola estudada em geometria analítica não é deficiente?
Na videoaula "28. Geometria Analítica - Equação da Parábola" (também disponível em meu
canal no YouTube), eu exibo que a equação
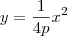
serve para representar as parábolas que possuem vértice na origem, eixo de simetria coincidindo com o eixo y e concavidade voltada para cima.
Entretanto, essas restrições não representam uma "deficiência". Isso porque sempre podemos efetuar translações e rotações de eixos de modo a obter essa equação básica. Ou seja, dada qualquer parábola de equação
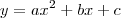
, podemos efetuar translações e rotações de eixos de modo a obter a equação básica
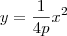
(que é muito mais simples de trabalhar do que a anterior). É exatamente por isso que estudamos translações e rotações de eixos em Geometria Analítica.
Jhenrique escreveu:E outra, eu vi um livro que traz a equação geral das cônicas como
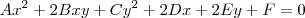
, certamente fazendo alusão ao produto notável:
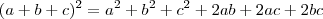
.
E então, que me dizem? Gostaria de
esclarecimentos!
Cada autor tem as suas preferências. Ambas as equações estão corretas no contexto usado por cada autor.
-

LuizAquino
- Colaborador Moderador - Professor

-
- Mensagens: 2654
- Registrado em: Sex Jan 21, 2011 09:11
- Localização: Teófilo Otoni - MG
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Mestrado - Modelagem Computacional
- Andamento: formado
-
 por Jhenrique » Seg Dez 17, 2012 12:30
por Jhenrique » Seg Dez 17, 2012 12:30
LuizAquino escreveu:Entretanto, essas restrições não representam uma "deficiência". Isso porque sempre podemos efetuar translações e rotações de eixos de modo a obter essa equação básica. Ou seja, dada qualquer parábola de equação
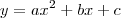
, podemos efetuar translações e rotações de eixos de modo a obter a equação básica
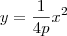
(que é muito mais simples de trabalhar do que a anterior). É exatamente por isso que estudamos translações e rotações de eixos em Geometria Analítica.
Muito bacana!
LuizAquino escreveu:Cada autor tem as suas preferências. Ambas as equações estão corretas no contexto usado por cada autor.
Mas
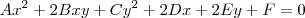
tem alguma utilidade algébrica?
---
Por fim, se não me esqueci de mais nenhuma pergunta, a última é a seguinte... conseguimos relacionar 4 tipos de equações com uma entidade geométrica, a cônica. Mas sabemos que a matemática possui muitos outros modelos de equações além das cônicas, esses outros modelos não estão relacionados com outras entidades geométricas também?
"A solução errada para o problema certo é anos-luz melhor do que a solução certa para o problema errado." - Russell Ackoff
-
Jhenrique
- Colaborador Voluntário

-
- Mensagens: 180
- Registrado em: Dom Mai 15, 2011 22:37
- Formação Escolar: ENSINO MÉDIO
- Área/Curso: Técnico em Mecânica
- Andamento: formado
 por LuizAquino » Seg Dez 17, 2012 15:40
por LuizAquino » Seg Dez 17, 2012 15:40
Jhenrique escreveu:Mas
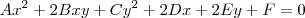
tem alguma utilidade algébrica?
Não. A mesma "utilidade algébrica" que essa tem, a outra também tem.
Jhenrique escreveu:Por fim, se não me esqueci de mais nenhuma pergunta, a última é a seguinte... conseguimos relacionar 4 tipos de equações com uma entidade geométrica, a cônica. Mas sabemos que a matemática possui muitos outros modelos de equações além das cônicas, esses outros modelos não estão relacionados com outras entidades geométricas também?
Dado um certo "modelo de equação", podemos obter uma "entidade geométrica" relacionada a ele (o seu "gráfico", por assim dizer).
A questão é: nos cursos de graduação nós apenas estudamos as "entidades geométricas" clássicas, que são amplamente aplicadas nos mais diversos problemas em Matemática, Física e Engenharia.
As "entidades geométricas" que "não são clássicas" podem ser estudadas por curiosidade ou para resolver um problema muito específico. Nesse contexto, elas não são abordadas nos cursos de graduação. Até porque, se em uma graduação fossemos estudar tudo de tudo com total detalhe, ao invés do curso durar 4 ou 5 anos ele duraria 20 ou 30! Ou até mais!
-

LuizAquino
- Colaborador Moderador - Professor

-
- Mensagens: 2654
- Registrado em: Sex Jan 21, 2011 09:11
- Localização: Teófilo Otoni - MG
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Mestrado - Modelagem Computacional
- Andamento: formado
-
 por Jhenrique » Seg Dez 17, 2012 21:35
por Jhenrique » Seg Dez 17, 2012 21:35
Entendi... bem, eu perguntei por curiosidade mesmo, na verdade, eu acho que tudo é importante, penso que é importante conhecer o todo a fim de ter um "baralho completo de cartas". Quero dizer, a curva evolvente não é um assunto estudado, porém Euler a conhecia muito bem as propriedades dessa curva "irrelevante" e sugeriu ela como perfil de dentes de engrenagens, esse perfil é usado até hoje em quase todas as engrenagens fabricadas!
"A solução errada para o problema certo é anos-luz melhor do que a solução certa para o problema errado." - Russell Ackoff
-
Jhenrique
- Colaborador Voluntário

-
- Mensagens: 180
- Registrado em: Dom Mai 15, 2011 22:37
- Formação Escolar: ENSINO MÉDIO
- Área/Curso: Técnico em Mecânica
- Andamento: formado
Voltar para Geometria Analítica
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Questão sobre cônicas
por Cristiano Tavares » Dom Set 04, 2011 12:41
- 1 Respostas
- 1201 Exibições
- Última mensagem por LuizAquino

Dom Set 04, 2011 20:11
Geometria Analítica
-
- Geometria Analítica [Dúvida] sobre cônicas
por pablohas » Sáb Dez 04, 2010 12:55
- 6 Respostas
- 5726 Exibições
- Última mensagem por pablohas

Seg Dez 06, 2010 20:17
Geometria Analítica
-
- [Cônicas]Retas tangentes à cônicas
por Hopkins » Ter Fev 28, 2017 22:39
- 0 Respostas
- 1526 Exibições
- Última mensagem por Hopkins

Ter Fev 28, 2017 22:39
Geometria Analítica
-
- Conicas
por baianinha » Qua Set 14, 2011 00:30
- 1 Respostas
- 1433 Exibições
- Última mensagem por LuizAquino

Qua Set 14, 2011 00:58
Álgebra Elementar
-
- Cônicas
 por Claudin » Dom Mai 13, 2012 12:43
por Claudin » Dom Mai 13, 2012 12:43
- 7 Respostas
- 3131 Exibições
- Última mensagem por Claudin

Dom Mai 20, 2012 23:08
Geometria Analítica
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
método de contagem
Autor:
sinuca147 - Seg Mai 25, 2009 09:10
Veja este exercício:
Se A = {

} e B = {

}, então o número de elementos A

B é:
Eu tentei resolver este exercício e achei a resposta "três", mas surgiram muitas dúvidas aqui durante a resolução.
Para determinar os elementos do conjunto A, eu tive de basicamente fazer um lista de vinte dividido por todos os números naturais maiores que zero e menores que vinte e um, finalmente identificando como elementos do conjunto A os números 1, 2, 4, 5, 10 e 20. Acho que procedi de maneira correta, mas fiquei pensando aqui se não existiria um método mais "sofisticado" e prático para que eu pudesse identificar ou ao menos contar o número de elementos do conjunto A, existe?
No processo de determinação dos elementos do conjunto B o que achei foi basicamente os múltiplos de cinco e seus opostos, daí me surgiram estas dúvidas:
existe oposto de zero?
existe inverso de zero?
zero é par, certo?
sendo x um número natural, -x é múltiplo de x?
sendo z um número inteiro negativo, z é múltiplo de z?
sendo z um número inteiro negativo, -z é múltiplo de z?
A resposta é 3?
Obrigado.
Assunto:
método de contagem
Autor:
Molina - Seg Mai 25, 2009 20:42
Boa noite, sinuca.
Se A = {

} você concorda que n só pode ser de 1 a 20? Já que pertence aos naturais?
Ou seja, quais são os divisores de 20? Eles são seis: 1, 2, 4, 5, 10 e 20.
Logo, o conjunto A é
A = {1, 2, 4, 5, 10, 20}
Se B = {

} você concorda que x será os múltiplos de 5 (positivos e negativos)? Já que m pertence ao conjunto Z?
Logo, o conjunto B é
B = {... , -25, -20, -15, -10, -5, 0, 5, 10, 15, 20, 25, ...
Feito isso precisamos ver os números que está em ambos os conjuntos, que são:
5, 10 e 20 (3 valores, como você achou).
Vou responder rapidamente suas dúvidas porque meu tempo está estourando. Qualquer dúvida, coloque aqui, ok?
sinuca147 escreveu:No processo de determinação dos elementos do conjunto B o que achei foi basicamente os múltiplos de cinco e seus opostos, daí me surgiram estas dúvidas:
existe oposto de zero? sim, é o próprio zero
existe inverso de zero? não, pois não há nenhum número que multiplicado por zero resulte em 1
zero é par, certo? sim, pois pode ser escrito da forma de 2n, onde n pertence aos inteiros
sendo x um número natural, -x é múltiplo de x? Sim, pois basta pegar x e multiplicar por -1 que encontramos -x
sendo z um número inteiro negativo, z é múltiplo de z? Sim, tais perguntando se todo número é multiplo de si mesmo
sendo z um número inteiro negativo, -z é múltiplo de z? Sim, pois basta pegar -z e multiplicar por -1 que encontramos x
A resposta é 3? Sim, pelo menos foi o que vimos a cima
Bom estudo,

Assunto:
método de contagem
Autor:
sinuca147 - Seg Mai 25, 2009 23:35
Obrigado, mas olha só este link
http://www.colegioweb.com.br/matematica ... ro-natural
neste link encontra-se a a frase:
Múltiplo de um número natural é qualquer número que possa ser obtido multiplicando o número natural por 0, 1, 2, 3, 4, 5, etc.
Para determinarmos os múltiplos de 15, por exemplo, devemos multiplicá-lo pela sucessão dos números naturais:
Ou seja, de acordo com este link -5 não poderia ser múltiplo de 5, assim como 5 não poderia ser múltiplo de -5, eu sempre achei que não interessava o sinal na questão dos múltiplos, assim como você me confirmou, mas e essa informação contrária deste site, tem alguma credibilidade?
Há e claro, a coisa mais bacana você esqueceu, quero saber se existe algum método de contagem diferente do manual neste caso:
Para determinar os elementos do conjunto A, eu tive de basicamente fazer um lista de vinte dividido por todos os números naturais maiores que zero e menores que vinte e um, finalmente identificando como elementos do conjunto A os números 1, 2, 4, 5, 10 e 20. Acho que procedi de maneira correta, mas fiquei pensando aqui se não existiria um método mais "sofisticado" e prático para que eu pudesse identificar ou ao menos contar o número de elementos do conjunto A, existe?
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
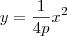

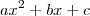 , portanto, a equação da parábola estudada em geometria analítica não é deficiente?
, portanto, a equação da parábola estudada em geometria analítica não é deficiente? 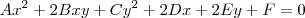 , certamente fazendo alusão ao produto notável:
, certamente fazendo alusão ao produto notável: 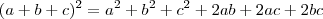 .
.

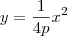 serve para representar as parábolas que possuem vértice na origem, eixo de simetria coincidindo com o eixo y e concavidade voltada para cima.
serve para representar as parábolas que possuem vértice na origem, eixo de simetria coincidindo com o eixo y e concavidade voltada para cima.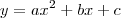 , podemos efetuar translações e rotações de eixos de modo a obter a equação básica
, podemos efetuar translações e rotações de eixos de modo a obter a equação básica 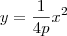 (que é muito mais simples de trabalhar do que a anterior). É exatamente por isso que estudamos translações e rotações de eixos em Geometria Analítica.
(que é muito mais simples de trabalhar do que a anterior). É exatamente por isso que estudamos translações e rotações de eixos em Geometria Analítica.
 } e B = {
} e B = { }, então o número de elementos A
}, então o número de elementos A  B é:
B é: