 por Danilo » Ter Nov 06, 2012 19:57
por Danilo » Ter Nov 06, 2012 19:57
Considere os vetores v = i+3j+2k, w = 2i-j+k e u = i-2j. Seja pi um plano paralelo aos vetores W e U e r uma reta perpendicular ao plano pi. Ache a projeção ortogonal do vetor V sobre a reta r, ou seja, a projeção ortogonal de V sobre o vetor diretor da reta r.
Bom, eu compreendi o enunciado até na parte em que chegou no plano pi.... aonde que entra o vetor v? Sendo que no exercício nada foi falado sobre ele? Ou há um erro no enunciado?
-
Danilo
- Colaborador Voluntário

-
- Mensagens: 224
- Registrado em: Qui Mar 15, 2012 23:36
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Matemática
- Andamento: cursando
 por LuizAquino » Qua Nov 07, 2012 10:07
por LuizAquino » Qua Nov 07, 2012 10:07
Danilo escreveu:Considere os vetores v = i+3j+2k, w = 2i-j+k e u = i-2j. Seja pi um plano paralelo aos vetores W e U e r uma reta perpendicular ao plano pi. Ache a projeção ortogonal do vetor V sobre a reta r, ou seja, a projeção ortogonal de V sobre o vetor diretor da reta r.
Bom, eu compreendi o enunciado até na parte em que chegou no plano pi.... aonde que entra o vetor v? Sendo que no exercício nada foi falado sobre ele? Ou há um erro no enunciado?
Não há erro no enunciado. O exercício pede claramente que seja determinada "(...)
a projeção ortogonal do vetor V sobre a reta r, ou seja, a projeção ortogonal de V sobre o vetor diretor da reta r".
A figura abaixo ilustra o exercício. O objetivo é determinar
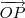
, que corresponde a projeção ortogonal de

sobre a reta r.
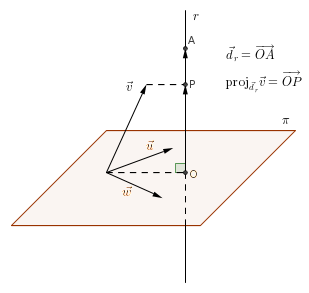
- figura.png (5.4 KiB) Exibido 5283 vezes
Agora tente concluir o exercício.
-

LuizAquino
- Colaborador Moderador - Professor

-
- Mensagens: 2654
- Registrado em: Sex Jan 21, 2011 09:11
- Localização: Teófilo Otoni - MG
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Mestrado - Modelagem Computacional
- Andamento: formado
-
 por Danilo » Qua Nov 07, 2012 11:10
por Danilo » Qua Nov 07, 2012 11:10
Professor, se eu fizer o produto vetorial entre os vetores paralelo ao plano, vou obter um vetor diretor da reta r, correto? Sendo assim basta concluir o exercício?
-
Danilo
- Colaborador Voluntário

-
- Mensagens: 224
- Registrado em: Qui Mar 15, 2012 23:36
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Matemática
- Andamento: cursando
 por LuizAquino » Qua Nov 07, 2012 16:16
por LuizAquino » Qua Nov 07, 2012 16:16
Danilo escreveu:Professor, se eu fizer o produto vetorial entre os vetores paralelo ao plano, vou obter um vetor diretor da reta r, correto? Sendo assim basta concluir o exercício?
Sim para as duas perguntas.
-

LuizAquino
- Colaborador Moderador - Professor

-
- Mensagens: 2654
- Registrado em: Sex Jan 21, 2011 09:11
- Localização: Teófilo Otoni - MG
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Mestrado - Modelagem Computacional
- Andamento: formado
-
Voltar para Geometria Analítica
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Projeção Ortogonal
por Balanar » Dom Out 24, 2010 18:19
- 0 Respostas
- 2095 Exibições
- Última mensagem por Balanar

Dom Out 24, 2010 18:19
Geometria Plana
-
- Mínimos quadrados e Projeção Ortogonal
por Jhonata » Sex Jul 19, 2013 19:44
- 7 Respostas
- 5226 Exibições
- Última mensagem por Jhonata

Dom Jul 21, 2013 10:49
Álgebra Linear
-
- Planos paralelos e projeção ortogonal
por dandara » Seg Dez 29, 2014 10:18
- 1 Respostas
- 2291 Exibições
- Última mensagem por adauto martins

Sex Jan 02, 2015 14:49
Geometria Espacial
-
- [operador linear] calcular projeção ortogonal
por Ge_dutra » Sáb Mar 16, 2013 19:42
- 0 Respostas
- 1558 Exibições
- Última mensagem por Ge_dutra

Sáb Mar 16, 2013 19:42
Álgebra Linear
-
- vetores e projeção
por cristina » Sex Mai 14, 2010 11:30
- 5 Respostas
- 3079 Exibições
- Última mensagem por DanielFerreira

Seg Jun 14, 2010 22:03
Geometria Analítica
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
dúvida em uma questão em regra de 3!
Autor:
leandro moraes - Qui Jul 01, 2010 12:41
pessoal eu achei como resultado 180 toneladas,entretanto sei que a questão está erra pela lógica e a resposta correta segundo o gabarito é 1.800 toneladas.
me explique onde eu estou pecando na questão. resolva explicando.
78 – ( CEFET – 1993 ) Os desabamentos, em sua maioria, são causados por grande acúmulo de lixo nas encostas dos morros. Se 10 pessoas retiram 135 toneladas de lixo em 9 dias, quantas toneladas serão retiradas por 40 pessoas em 30 dias ?
Assunto:
dúvida em uma questão em regra de 3!
Autor:
Douglasm - Qui Jul 01, 2010 13:16
Observe o raciocínio:
10 pessoas - 9 dias - 135 toneladas
1 pessoa - 9 dias - 13,5 toneladas
1 pessoa - 1 dia - 1,5 toneladas
40 pessoas - 1 dia - 60 toneladas
40 pessoas - 30 dias - 1800 toneladas
Assunto:
dúvida em uma questão em regra de 3!
Autor:
leandro moraes - Qui Jul 01, 2010 13:18
pessoal já achei a resposta. o meu erro foi bobo rsrsrrs errei em uma continha de multiplicação, é mole rsrsrsr mas felizmente consegui.
Assunto:
dúvida em uma questão em regra de 3!
Autor:
leandro moraes - Qui Jul 01, 2010 13:21
leandro moraes escreveu:pessoal já achei a resposta. o meu erro foi bobo rsrsrrs errei em uma continha de multiplicação, é mole rsrsrsr mas felizmente consegui.
valeu meu camarada.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.


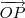 , que corresponde a projeção ortogonal de
, que corresponde a projeção ortogonal de  sobre a reta r.
sobre a reta r.