Dado os pontos P1 (2;-1) e P2 (-2;1), determine todos os pontos S pertencente a parábola
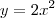 tal que P1S seja perpendicular a P2S.
tal que P1S seja perpendicular a P2S.Obrigado.

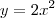 tal que P1S seja perpendicular a P2S.
tal que P1S seja perpendicular a P2S.
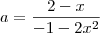
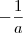
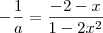
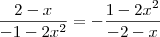
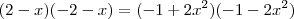

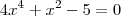


Voltar para Geometria Analítica
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante