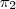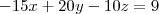por young_jedi » Qui Out 11, 2012 20:55
por young_jedi » Qui Out 11, 2012 20:55
significa que a segunda equação é combinação linear da outra
isso quer dizer ou que os planos são coincidentes ou são paralelos
neste caso eles são paralelos.
note que se voce multiplicar
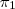
por -5 voce tera

comparando com
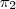
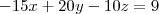
da para ver que eles são paralelos
-
young_jedi
- Colaborador Voluntário

-
- Mensagens: 1239
- Registrado em: Dom Set 09, 2012 10:48
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica - UEL
- Andamento: formado
 por MrJuniorFerr » Qui Out 11, 2012 21:01
por MrJuniorFerr » Qui Out 11, 2012 21:01
Entendi young_jedi, só varia o valor de d.
Mas enfim, com este fato, como eu determino a interseção de dois planos paralelos?
-

MrJuniorFerr
- Colaborador Voluntário

-
- Mensagens: 119
- Registrado em: Qui Set 20, 2012 16:51
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia de Alimentos
- Andamento: cursando
 por young_jedi » Qui Out 11, 2012 21:05
por young_jedi » Qui Out 11, 2012 21:05
isso mesmo só o de não varia por isso eles são paralelos se o d fosse igual seriam o mesmo plano
bom nesse caso, a intersecção deles não existe, se são paralelos não existe nem um ponto deles que seja comum.
-
young_jedi
- Colaborador Voluntário

-
- Mensagens: 1239
- Registrado em: Dom Set 09, 2012 10:48
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica - UEL
- Andamento: formado
 por MrJuniorFerr » Qui Out 11, 2012 21:17
por MrJuniorFerr » Qui Out 11, 2012 21:17
young_jedi escreveu:isso mesmo só o de não varia por isso eles são paralelos se o d fosse igual seriam o mesmo plano
bom nesse caso, a intersecção deles não existe, se são paralelos não existe nem um ponto deles que seja comum.
Neste caso pude perceber que os dois planos não há pontos em comum devido ao acontecimento estranho no escalonamento. Mas em nenhum outro caso eles terão pontos em comum? Difícil imaginar que todos planos paralelos não possam coincidir.
-

MrJuniorFerr
- Colaborador Voluntário

-
- Mensagens: 119
- Registrado em: Qui Set 20, 2012 16:51
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia de Alimentos
- Andamento: cursando
 por young_jedi » Qui Out 11, 2012 21:21
por young_jedi » Qui Out 11, 2012 21:21
se os planos são paralelos eles não se encontram.
Coloque duas folhas de sufite paralelas mesmo que voce estenda seus tamanhos para o infinito elas nunca se encontram
é o mesmo com as retas paralelas.
se eles se coicidem é o mesmo plano na verdade
-
young_jedi
- Colaborador Voluntário

-
- Mensagens: 1239
- Registrado em: Dom Set 09, 2012 10:48
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica - UEL
- Andamento: formado
 por MrJuniorFerr » Qui Out 11, 2012 21:26
por MrJuniorFerr » Qui Out 11, 2012 21:26
É possível planos serem paralelos e colineares?
Se forem paralelos e colineares, na verdade é o mesmo plano?
Editado pela última vez por
MrJuniorFerr em Qui Out 11, 2012 21:34, em um total de 1 vez.
-

MrJuniorFerr
- Colaborador Voluntário

-
- Mensagens: 119
- Registrado em: Qui Set 20, 2012 16:51
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia de Alimentos
- Andamento: cursando
 por young_jedi » Qui Out 11, 2012 21:32
por young_jedi » Qui Out 11, 2012 21:32
se a equação de dois planos forem colineares isso signifca que eles representam o mesmo plano no espaço.
ou seja se são coplanares representam o mesmo plano
-
young_jedi
- Colaborador Voluntário

-
- Mensagens: 1239
- Registrado em: Dom Set 09, 2012 10:48
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica - UEL
- Andamento: formado
 por MrJuniorFerr » Qui Out 11, 2012 21:39
por MrJuniorFerr » Qui Out 11, 2012 21:39
Entendi young_jedi. Vou continuar aqui com os meus exercícios.
Obrigado pela ajuda!
-

MrJuniorFerr
- Colaborador Voluntário

-
- Mensagens: 119
- Registrado em: Qui Set 20, 2012 16:51
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia de Alimentos
- Andamento: cursando
Voltar para Geometria Analítica
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [Equação de planos] Dúvida exercício
por MrJuniorFerr » Sáb Out 06, 2012 17:16
- 2 Respostas
- 3952 Exibições
- Última mensagem por MrJuniorFerr

Sáb Out 06, 2012 18:19
Geometria Analítica
-
- [Equação de planos] Dùvida exercício 2
por MrJuniorFerr » Sáb Out 06, 2012 20:39
- 14 Respostas
- 9080 Exibições
- Última mensagem por young_jedi

Dom Out 07, 2012 19:07
Geometria Analítica
-
- [Equação de planos] Dùvida exercício 3
por MrJuniorFerr » Dom Out 07, 2012 02:49
- 3 Respostas
- 2331 Exibições
- Última mensagem por young_jedi

Dom Out 07, 2012 17:21
Geometria Analítica
-
- [Equação de planos] Dúvida exercício 4
por MrJuniorFerr » Seg Out 08, 2012 07:40
- 1 Respostas
- 1340 Exibições
- Última mensagem por young_jedi

Seg Out 08, 2012 10:06
Geometria Analítica
-
- [Equação de planos] Dúvida exercício 5
por MrJuniorFerr » Qui Out 11, 2012 08:58
- 4 Respostas
- 2131 Exibições
- Última mensagem por MrJuniorFerr

Qui Out 11, 2012 12:43
Geometria Analítica
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
Taxa de variação
Autor:
felipe_ad - Ter Jun 29, 2010 19:44
Como resolvo uma questao desse tipo:
Uma usina de britagem produz pó de pedra, que ao ser depositado no solo, forma uma pilha cônica onde a altura é aproximadamente igual a 4/3 do raio da base.
(a) Determinar a razão de variação do volume em relação ao raio da base.
(b) Se o raio da base varia a uma taxa de 20 cm/s, qual a razão de variação do volume quando o raio mede 2 m?
A letra (a) consegui resolver e cheguei no resultado correto de

Porem, nao consegui chegar a um resultado correto na letra (b). A resposta certa é

Alguem me ajuda? Agradeço desde já.
Assunto:
Taxa de variação
Autor:
Elcioschin - Qua Jun 30, 2010 20:47
V = (1/3)*pi*r²*h ----> h = 4r/3
V = (1/3)*pi*r²*(4r/3) ----> V = (4*pi/9)*r³
Derivando:
dV/dr = (4*pi/9)*(3r²) -----> dV/dr = 4pi*r²/3
Para dr = 20 cm/s = 0,2 m/s e R = 2 m ----> dV/0,2 = (4*pi*2²)/3 ----> dV = (3,2/3)*pi ----> dV ~= 1,066*pi m³/s
Assunto:
Taxa de variação
Autor:
Guill - Ter Fev 21, 2012 21:17
Temos que o volume é dado por:

Temos, portanto, o volume em função do raio. Podemos diferenciar implicitamente ambos os lados da equação em função do tempo, para encontrar as derivadas em função do tempo:

Sabendo que a taxa de variação do raio é 0,2 m/s e que queremos ataxa de variação do volume quando o raio for 2 m:


Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
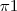 e
e 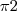 . Quando se tratar de uma reta, descreva-a por equações paramétricas.
. Quando se tratar de uma reta, descreva-a por equações paramétricas.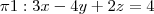 e
e 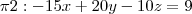
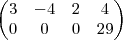

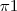 e
e 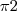 . Quando se tratar de uma reta, descreva-a por equações paramétricas.
. Quando se tratar de uma reta, descreva-a por equações paramétricas.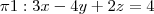 e
e 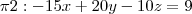

 por -5 voce tera
por -5 voce tera