 por iarapassos » Qua Ago 29, 2012 12:39
por iarapassos » Qua Ago 29, 2012 12:39
Eu tentei resolver usando projeção. Já que tenho um vetor // a ao AC, usei então o sei versor. versor de u= + ou - versor de AC. Também sei que a diagonal AC =AB+AD.
Mas depois que achei o vetor AO que seria o centro do losango, não sei mais como desenvolver para achar os valores das coordenadas... Me ajudem, please!

De um losango ABCD sabemos que A(1,0,2), B(2,-1,2) e a diagonal AC é paralela ao vetor u=(-1,2,2). Determine as coordenadas dos outros vértices.
-
iarapassos
- Usuário Ativo

-
- Mensagens: 23
- Registrado em: Qua Ago 29, 2012 12:34
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia de Controle e Automação
- Andamento: cursando
 por LuizAquino » Qua Ago 29, 2012 19:37
por LuizAquino » Qua Ago 29, 2012 19:37
iarapassos escreveu:Eu tentei resolver usando projeção. Já que tenho um vetor // a ao AC, usei então o sei versor. versor de u= + ou - versor de AC. Também sei que a diagonal AC =AB+AD.
Mas depois que achei o vetor AO que seria o centro do losango, não sei mais como desenvolver para achar os valores das coordenadas... Me ajudem, please!

De um losango ABCD sabemos que A(1,0,2), B(2,-1,2) e a diagonal AC é paralela ao vetor u=(-1,2,2). Determine as coordenadas dos outros vértices.
Faça o seguinte:
1) calcule o vetor
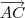
através da relação
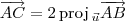
;
2) determine C usando a relação

;
3) determine D usando a relação

.
-

LuizAquino
- Colaborador Moderador - Professor

-
- Mensagens: 2654
- Registrado em: Sex Jan 21, 2011 09:11
- Localização: Teófilo Otoni - MG
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Mestrado - Modelagem Computacional
- Andamento: formado
-
Voltar para Geometria Analítica
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [Geometria Analítica] Projeção do ponto no plano
 por -civil- » Qui Ago 11, 2011 09:51
por -civil- » Qui Ago 11, 2011 09:51
- 1 Respostas
- 2989 Exibições
- Última mensagem por LuizAquino

Sex Ago 12, 2011 13:14
Geometria Analítica
-
- Geometria Analítica
por maysa » Ter Abr 14, 2009 10:35
- 1 Respostas
- 7691 Exibições
- Última mensagem por Marcampucio

Ter Abr 14, 2009 15:52
Geometria Analítica
-
- GEOMETRIA ANALITICA
por GABRIELA » Ter Set 29, 2009 17:20
- 3 Respostas
- 5452 Exibições
- Última mensagem por GABRIELA

Qua Set 30, 2009 16:49
Geometria Analítica
-
- Geometria analítica
por shirata » Qua Nov 11, 2009 20:37
- 2 Respostas
- 4178 Exibições
- Última mensagem por shirata

Dom Nov 15, 2009 09:25
Geometria Espacial
-
- geometria analitica
por Jaison Werner » Sex Abr 23, 2010 21:19
- 3 Respostas
- 3960 Exibições
- Última mensagem por MarceloFantini

Dom Jun 13, 2010 19:03
Geometria Analítica
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
Unesp - 95 Números Complexos
Autor:
Alucard014 - Dom Ago 01, 2010 18:22
(UNESP - 95) Seja L o Afixo de um Número complexo

em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto.
Assunto:
Unesp - 95 Números Complexos
Autor:
MarceloFantini - Qui Ago 05, 2010 17:27
Seja

o ângulo entre o eixo horizontal e o afixo

. O triângulo é retângulo com catetos

e

, tal que

. Seja

o ângulo complementar. Então

. Como

, o ângulo que o afixo

formará com a horizontal será

, mas negativo pois tem de ser no quarto quadrante. Se

, então

. Como módulo é um:

.
Logo, o afixo é

.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.



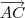 através da relação
através da relação 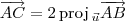 ;
; ;
; .
.
 em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto.
em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto. o ângulo entre o eixo horizontal e o afixo
o ângulo entre o eixo horizontal e o afixo  . O triângulo é retângulo com catetos
. O triângulo é retângulo com catetos  e
e  , tal que
, tal que  . Seja
. Seja  o ângulo complementar. Então
o ângulo complementar. Então  . Como
. Como  , o ângulo que o afixo
, o ângulo que o afixo  formará com a horizontal será
formará com a horizontal será  , então
, então  . Como módulo é um:
. Como módulo é um:  .
. .
.