(Fuvest)No plano cartesiano, considere o quadrado de vértices A= (0,0) , B = (a,0), C (0,a) e D (a,a), onde a>0. sabendo-se que os triângulos ABE, com E no interior do quadrado, e BDF, com F no exterior do quadrado, são triângulos equiláteros, prove que os pontos C, E e F estão alinhados.
eu sei que para que não exista triangulo o determinante é igual a zero e assim os pontos estão alinhados . Mas como poder haver triangulo (determinante diferente de zero , eu suponho) se os pontos estão alinhados (determinante igual a zero) ?? com essa dúvida nao consigo nem montar o determinante ... Bem , eu não consegui , se alguém puder me orientar fico muito grata ...


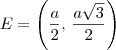
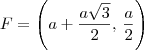


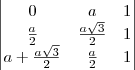
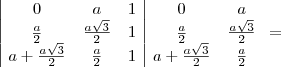
![= \left[0\cdot \frac{a\sqrt{3}}{2} \cdot 1 + a\cdot 1 \cdot \left(a + \frac{a\sqrt{3}}{2}\right) + 1\cdot \frac{a}{2}\cdot \frac{a}{2}\right] - \left[1\cdot \frac{a\sqrt{3}}{2} \cdot \left(a + \frac{a\sqrt{3}}{2}\right) + 0 \cdot 1 \cdot \frac{a}{2} + a\cdot \frac{a}{2}\cdot 1\right] = \left[0\cdot \frac{a\sqrt{3}}{2} \cdot 1 + a\cdot 1 \cdot \left(a + \frac{a\sqrt{3}}{2}\right) + 1\cdot \frac{a}{2}\cdot \frac{a}{2}\right] - \left[1\cdot \frac{a\sqrt{3}}{2} \cdot \left(a + \frac{a\sqrt{3}}{2}\right) + 0 \cdot 1 \cdot \frac{a}{2} + a\cdot \frac{a}{2}\cdot 1\right]](/latexrender/pictures/7a55eaed875389280ed08f6aeaa0d29e.png)
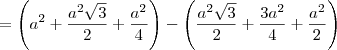
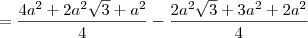
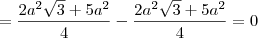
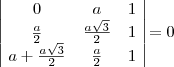
 .
. ,
,  e para
e para  ,
,  .
.
 e
e  , monte a função e substitua
, monte a função e substitua  por
por  .
.
