 por Claudin » Sex Abr 27, 2012 01:41
por Claudin » Sex Abr 27, 2012 01:41
Determine a reta que contém o ponto (2,-3) e forma 60º com eivo Ox.
Não sei concluir o exercício.
"O que sabemos é uma gota, o que não sabemos é um oceano." - Isaac Newton
-
Claudin
- Colaborador Voluntário

-
- Mensagens: 913
- Registrado em: Qui Mai 12, 2011 17:34
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica
- Andamento: cursando
 por LuizAquino » Sex Abr 27, 2012 02:32
por LuizAquino » Sex Abr 27, 2012 02:32
Claudin escreveu:Determine a reta que contém o ponto (2,-3) e forma 60º com eivo Ox.
Claudin escreveu:Não sei concluir o exercício.
Há várias formas de fazer esse exercício.
Se for para usar os conhecimentos sobre vetores diretores, então você pode fazer o seguinte.
Note que se a reta forma 60º com o eixo Ox, então um vetor diretor para essa reta é
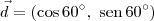
. Ou seja, um vetor diretor é
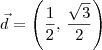
.
Agora tente concluir o exercício a partir daí.
-

LuizAquino
- Colaborador Moderador - Professor

-
- Mensagens: 2654
- Registrado em: Sex Jan 21, 2011 09:11
- Localização: Teófilo Otoni - MG
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Mestrado - Modelagem Computacional
- Andamento: formado
-
 por Claudin » Sáb Abr 28, 2012 17:10
por Claudin » Sáb Abr 28, 2012 17:10
A equação paramétrica seria:
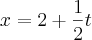
![y= -3 + \frac{\sqrt[]{3}}{2}t y= -3 + \frac{\sqrt[]{3}}{2}t](/latexrender/pictures/39e3da8c991b590fed51b69cd78fa997.png)
Mas gostaria de saber na forma CARTESIANA agora, como que fica?
"O que sabemos é uma gota, o que não sabemos é um oceano." - Isaac Newton
-
Claudin
- Colaborador Voluntário

-
- Mensagens: 913
- Registrado em: Qui Mai 12, 2011 17:34
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica
- Andamento: cursando
 por LuizAquino » Dom Abr 29, 2012 11:53
por LuizAquino » Dom Abr 29, 2012 11:53
Claudin escreveu:A equação paramétrica seria:
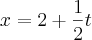
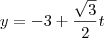
Mas gostaria de saber na forma CARTESIANA agora, como que fica?
Simples. Comece isolando a variável t na primeira equação:
t = 2x - 4
Agora substitua t na segunda equação:
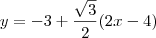
Por fim, arrumando a equação temos que:
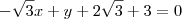
-

LuizAquino
- Colaborador Moderador - Professor

-
- Mensagens: 2654
- Registrado em: Sex Jan 21, 2011 09:11
- Localização: Teófilo Otoni - MG
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Mestrado - Modelagem Computacional
- Andamento: formado
-
 por Claudin » Dom Abr 29, 2012 13:14
por Claudin » Dom Abr 29, 2012 13:14
"O que sabemos é uma gota, o que não sabemos é um oceano." - Isaac Newton
-
Claudin
- Colaborador Voluntário

-
- Mensagens: 913
- Registrado em: Qui Mai 12, 2011 17:34
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica
- Andamento: cursando
Voltar para Geometria Analítica
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- geometria analítica estudo da reta distancia do ponta à reta
por jeffersonricardo » Dom Ago 22, 2010 08:29
- 1 Respostas
- 2304 Exibições
- Última mensagem por Pedro123

Seg Ago 23, 2010 22:24
Geometria Analítica
-
- [Equação da Reta] Reta que passa por pontos do plano.
por acorreia » Qua Mai 02, 2012 17:31
- 1 Respostas
- 2374 Exibições
- Última mensagem por Russman

Qua Mai 02, 2012 21:25
Geometria Analítica
-
- [ESTUDO DA RETA] Ponto da reta, com os pontos A e B sendo eq
 por rochadapesada » Dom Dez 15, 2013 16:31
por rochadapesada » Dom Dez 15, 2013 16:31
- 8 Respostas
- 5074 Exibições
- Última mensagem por rochadapesada

Dom Dez 15, 2013 21:14
Geometria Analítica
-
- [DERIVADA] Reta tangente e Reta perpendicular
por antonelli2006 » Ter Nov 22, 2011 11:21
- 1 Respostas
- 8557 Exibições
- Última mensagem por LuizAquino

Ter Nov 22, 2011 14:28
Cálculo: Limites, Derivadas e Integrais
-
- [GA - Estudo da Reta] Exercício de GA com reta e plano
por matheus0807 » Qui Jun 05, 2014 15:12
- 0 Respostas
- 2018 Exibições
- Última mensagem por matheus0807

Qui Jun 05, 2014 15:12
Geometria Analítica
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
cálculo de limites
Autor:
Hansegon - Seg Ago 25, 2008 11:29
Bom dia.
Preciso de ajuda na solução deste problema, pois só chego ao resultado de 0 sobre 0.
Obrigado
\lim_{x\rightarrow-1} x³ +1/x²-1[/tex]
Assunto:
cálculo de limites
Autor:
Molina - Seg Ago 25, 2008 13:25

Realmente se você jogar o -1 na equação dá 0 sobre 0.
Indeterminações deste tipo você pode resolver por L'Hôpital
que utiliza derivada.
Outro modo é transformar o numerador e/ou denominador
para que não continue dando indeterminado.
Dica: dividir o numerador e o denominador por algum valor é uma forma que normalmente dá certo.

Caso ainda não tenha dado uma

, avisa que eu resolvo.
Bom estudo!
Assunto:
cálculo de limites
Autor:
Guill - Dom Abr 08, 2012 16:03



Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.



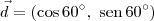 . Ou seja, um vetor diretor é
. Ou seja, um vetor diretor é 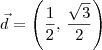 .
.
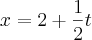
![y= -3 + \frac{\sqrt[]{3}}{2}t y= -3 + \frac{\sqrt[]{3}}{2}t](/latexrender/pictures/39e3da8c991b590fed51b69cd78fa997.png)

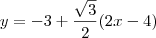
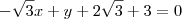




 , avisa que eu resolvo.
, avisa que eu resolvo.

