Mostre que os pontos (0,1,-1), (1,3,0) e (2,5,1) são colineares.
Também não consegui resolver esse exercício, fiz um com dois pontos, ai fiz uma relação de proporcionalidade entre os pontos e deu certo.
Agora com os três pontos não deu certo.



 tal que:
tal que: .(vetor BC)
.(vetor BC) .(1,2,1)
.(1,2,1) =1
=1
Lucio Carvalho escreveu:os vetores AB e BC (nota: falta a seta)
[tex]\vec{AB}[/tex]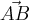
[tex]\overrightarrow{AB}[/tex]
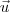 . Já a Forma 2) é mais interessante de ser usada quando temos duas letras em maiúsculo:
. Já a Forma 2) é mais interessante de ser usada quando temos duas letras em maiúsculo:  .
.

Voltar para Geometria Analítica
Usuários navegando neste fórum: Nenhum usuário registrado e 2 visitantes
![\frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}} \frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}}](/latexrender/pictures/981987c7bcdf9f8f498ca4605785636a.png)
![\sqrt[]{2} \sqrt[]{2}](/latexrender/pictures/f21662d1cabab6e8b273a4b6f1cd663a.png) (dica : igualar a expressão a
(dica : igualar a expressão a  e elevar ao quadrado os dois lados)
e elevar ao quadrado os dois lados)