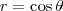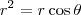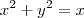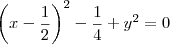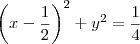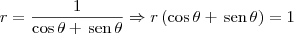Priscila_moraes escreveu:Olá pessoal precisa da ajuda de vocês como posso transformas a equação abaixo em coordenada cartesiana e identificar sua curva
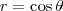
e
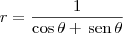
Lembre-se que as relações entre o ponto
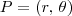
em coordenadas polares com o seu equivalente
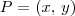
em coordenadas cartesianas são:
(i)
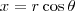
;
(ii)
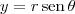
;
(iii)
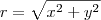
;
(iv)
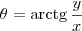
, caso
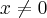
.
Para transformar as equações dadas em coordenadas polares para as suas equivalentes em coordenadas cartesianas, você deve fazer manipulações para fazer aparecer as relações acima.
Por exemplo, considere a primeira equação:
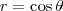
Multiplicando toda a equação por r, temos que:
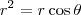
Lembrando-se das relações (i) e (iii), temos que:
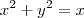

Completando quadrados em relação a variável x, temos que:
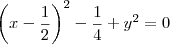
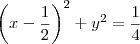
Essa equação representa uma circunferência de raio 1/2 e centro (1/2, 0).
Agora tente transformar a segunda equação. Comece percebendo que:
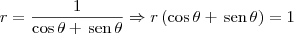
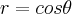
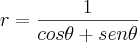

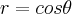
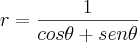

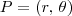 em coordenadas polares com o seu equivalente
em coordenadas polares com o seu equivalente 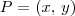 em coordenadas cartesianas são:
em coordenadas cartesianas são: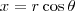 ;
;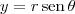 ;
;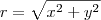 ;
;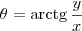 , caso
, caso 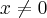 .
.