 por bobkaladao » Dom Nov 06, 2011 20:18
por bobkaladao » Dom Nov 06, 2011 20:18
Boa noite galera.
Estou em dúvida de como começar esse exercício:
Qual é o valor de m para que a área do paralelogramo
determinado pelos vetores u= (0, -3, 1) e v= (1, m, 0) seja
igual a raiz quadrada de 26?Como eu elaboro essa questão? Faço |U x V|=
![\sqrt[2]{26} \sqrt[2]{26}](/latexrender/pictures/9aacb797e265cf7ebda60007e7eaed78.png)
?
Ou faço o |U x V| e no resultado da matriz eu igualo a
![\sqrt[2]{26} \sqrt[2]{26}](/latexrender/pictures/9aacb797e265cf7ebda60007e7eaed78.png)
?
E mais um favor, se conhecerem algum bom material sobre vetores que possam me indicar eu agradeceria muito, pois estou meio perdido nesta matéria.
Obrigado.
-
bobkaladao
- Novo Usuário

-
- Mensagens: 1
- Registrado em: Seg Out 31, 2011 00:08
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia
- Andamento: cursando
 por LuizAquino » Dom Nov 06, 2011 23:17
por LuizAquino » Dom Nov 06, 2011 23:17
bobkaladao escreveu:Qual é o valor de m para que a área do paralelogramo
determinado pelos vetores u= (0, -3, 1) e v= (1, m, 0) seja
igual a raiz quadrada de 26?Como eu elaboro essa questão? Faço |U x V|=
![\sqrt[2]{26} \sqrt[2]{26}](/latexrender/pictures/9aacb797e265cf7ebda60007e7eaed78.png)
?
Sim, é assim que você deve iniciar.
bobkaladao escreveu:Ou faço o |U x V| e no resultado da matriz eu igualo a
![\sqrt[2]{26} \sqrt[2]{26}](/latexrender/pictures/9aacb797e265cf7ebda60007e7eaed78.png)
?
Quando você diz "resultado da matriz", suponho que você está se referindo ao determinante com o qual você calcularia

. Ou seja, o resultado do determinante:
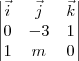
Note que o resultado desse determinante é um
vetor. Sendo assim, não faz sentido igualá-lo ao
escalar 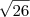
.
Por outro lado, ao calcular o
módulo de um vetor obtemos um escalar. Dessa forma, faz sentido escrever
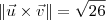
.
Em resumo:

é um vetor;
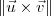
é um escalar.
bobkaladao escreveu:E mais um favor, se conhecerem algum bom material sobre vetores que possam me indicar eu agradeceria muito, pois estou meio perdido nesta matéria.
Eu recomendo o livro "Matrizes, Vetores e Geometria Analítica" de Reginaldo J. Santos. Ele está disponível na página pessoal de Santos:
Reginaldo J. Santoshttp://www.mat.ufmg.br/~regi/Além desse livro, eu também recomendo:
- Reis, Genésio; Silva, Valdir. Geometria Analítica. 2ª Edição. Rio de Janeiro: Editora LTC, 1996.
- Boulo, Paulo; Camargo, Ivan de. Geometria analítica: um tratamento vetorial. 3ª Edição. São Paulo: Pearson Prentice Hall, 2005.
-

LuizAquino
- Colaborador Moderador - Professor

-
- Mensagens: 2654
- Registrado em: Sex Jan 21, 2011 09:11
- Localização: Teófilo Otoni - MG
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Mestrado - Modelagem Computacional
- Andamento: formado
-
Voltar para Geometria Analítica
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [VETORES] Produto Vetorial
por IsadoraOliveira » Sex Set 28, 2012 16:23
- 1 Respostas
- 1970 Exibições
- Última mensagem por Russman

Sex Set 28, 2012 17:51
Geometria Analítica
-
- [Produto entre vetores] Escalar e vetorial
por ViniciusAlmeida » Qui Abr 23, 2015 23:36
- 1 Respostas
- 3116 Exibições
- Última mensagem por DanielFerreira

Sex Abr 24, 2015 21:24
Geometria Analítica
-
- Produto Vetorial - Medida angular entre os vetores
por talesalberto » Seg Nov 03, 2014 21:42
- 1 Respostas
- 2256 Exibições
- Última mensagem por Russman

Ter Nov 04, 2014 01:31
Geometria Analítica
-
- [Produto vetorial] Dúvida exercício
por MrJuniorFerr » Seg Out 29, 2012 13:52
- 4 Respostas
- 2621 Exibições
- Última mensagem por MarceloFantini

Seg Out 29, 2012 18:00
Geometria Analítica
-
- Produto escalar, Produto Vetorial e Produto Misto
 por fernando7 » Qua Mai 23, 2018 17:29
por fernando7 » Qua Mai 23, 2018 17:29
- 0 Respostas
- 4949 Exibições
- Última mensagem por fernando7

Qua Mai 23, 2018 17:29
Geometria Analítica
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
dúvida em uma questão em regra de 3!
Autor:
leandro moraes - Qui Jul 01, 2010 12:41
pessoal eu achei como resultado 180 toneladas,entretanto sei que a questão está erra pela lógica e a resposta correta segundo o gabarito é 1.800 toneladas.
me explique onde eu estou pecando na questão. resolva explicando.
78 – ( CEFET – 1993 ) Os desabamentos, em sua maioria, são causados por grande acúmulo de lixo nas encostas dos morros. Se 10 pessoas retiram 135 toneladas de lixo em 9 dias, quantas toneladas serão retiradas por 40 pessoas em 30 dias ?
Assunto:
dúvida em uma questão em regra de 3!
Autor:
Douglasm - Qui Jul 01, 2010 13:16
Observe o raciocínio:
10 pessoas - 9 dias - 135 toneladas
1 pessoa - 9 dias - 13,5 toneladas
1 pessoa - 1 dia - 1,5 toneladas
40 pessoas - 1 dia - 60 toneladas
40 pessoas - 30 dias - 1800 toneladas
Assunto:
dúvida em uma questão em regra de 3!
Autor:
leandro moraes - Qui Jul 01, 2010 13:18
pessoal já achei a resposta. o meu erro foi bobo rsrsrrs errei em uma continha de multiplicação, é mole rsrsrsr mas felizmente consegui.
Assunto:
dúvida em uma questão em regra de 3!
Autor:
leandro moraes - Qui Jul 01, 2010 13:21
leandro moraes escreveu:pessoal já achei a resposta. o meu erro foi bobo rsrsrrs errei em uma continha de multiplicação, é mole rsrsrsr mas felizmente consegui.
valeu meu camarada.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
![\sqrt[2]{26} \sqrt[2]{26}](/latexrender/pictures/9aacb797e265cf7ebda60007e7eaed78.png) ?
?![\sqrt[2]{26} \sqrt[2]{26}](/latexrender/pictures/9aacb797e265cf7ebda60007e7eaed78.png) ?
?

 . Ou seja, o resultado do determinante:
. Ou seja, o resultado do determinante: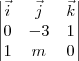
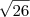 .
.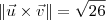 .
.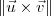 é um escalar.
é um escalar.