geo_nascimento escreveu:não consigo realizar umas questões de elipse e hipérbole ela tem cara de fácil mas pra mim é uma pedra no sapato:
De fato, as duas questões são fáceis como você verá a seguir. É só trabalhar com as definições e características das cônicas.
Determinar a equação da elipse de centro C(0,0), focos no eixo de x, excentricidade e=2/3 e passa pelo ponto P(2,-5/3).
A equação dessa elipse tem o formato:
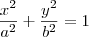
, sendo
a e
b números positivos e não nulos.
Por
definição, sabemos que sua excentricidade é dada pela relação:
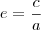
, sendo que

e
a >
b .
Sendo assim, dos dados do exercício temos a equação:

O outro dado do exercício diz que a elipse passa pelo ponto (2, -5/3). Isso significa que esse ponto deve atender a equação da elipse. Isto é, podemos escrever que:

Considerando então as duas equações que foram obtidas, para resolver o exercício basta calcular a solução do sistema:

Agora tente terminar a resolução.
Determine o centro, focos, semi-eixos, assíntota e reta diretriz (se houver) da equação 9x²-58y²+18y+29=0.
Será necessário arrumar a equação para que ele fique no formato reduzido. Para isso, nesse caso deve-se completar quadrados em relação a variável
y.


![9x^2 - 58\left[\left(y - \frac{9}{58}\right)^2 - \left(\frac{9}{58}\right)^2\right] + 29=0 9x^2 - 58\left[\left(y - \frac{9}{58}\right)^2 - \left(\frac{9}{58}\right)^2\right] + 29=0](/latexrender/pictures/bdb47d559860881f982236c706216f7c.png)


Dividindo toda essa equação por

:

Note que essa equação representa uma hipérbole.
Agora tente identificar as características solicitadas.


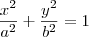 , sendo
, sendo 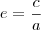 , sendo que
, sendo que  e
e 




![9x^2 - 58\left[\left(y - \frac{9}{58}\right)^2 - \left(\frac{9}{58}\right)^2\right] + 29=0 9x^2 - 58\left[\left(y - \frac{9}{58}\right)^2 - \left(\frac{9}{58}\right)^2\right] + 29=0](/latexrender/pictures/bdb47d559860881f982236c706216f7c.png)


 :
:
