Olá a todos,
Não estou conseguindo fazer uma questão sobre cônicas que pede a equação do lugar geométrico dos pontos M do plano não pertencentes à reta AB, tais que o ângulo B do triângulo AMB seja sempre o dobro do ângulo A do mesmo triângulo. As coordenadas dos pontos são A(-1,0) e B(2,0).
Saudações,
Cristiano Tavares
Salvado-BA


 o ângulo
o ângulo 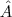 . Queremos que o ângulo
. Queremos que o ângulo 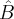 seja
seja 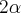 .
.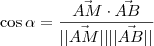
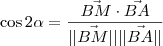
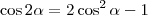 .
.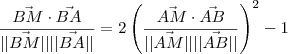

![\frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}} \frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}}](/latexrender/pictures/981987c7bcdf9f8f498ca4605785636a.png)
![\sqrt[]{2} \sqrt[]{2}](/latexrender/pictures/f21662d1cabab6e8b273a4b6f1cd663a.png)
 e elevar ao quadrado os dois lados)
e elevar ao quadrado os dois lados)