Olá a todos,
Não estou conseguindo resolver uma questão sobre cônicas. Nessa questão são dados cinco pontos que pertencem à cônica: P(1,1), Q(2,1), R(3,-1), S(-3,2) e T(-2,-1). Pergunta-se então qual é a equação da cônica.
Sei que a forma geral da equação de uma cônica (parábola, elipse, hipérbole) é Ax² + Bxy + Cy² + Dx + Ey + F = 0. Sei também que os pontos dados acima devem ser substituídos nessa equação geral, encontrando-se então um sistema de cinco equações com as incógnitas A, B, C, D, E, e F. O problema é que não estou conseguindo resolver esse sistema, não estou entendendo o fato de serem seis variáveis e apenas cinco equações.
Alguém poderia me ajudar a resolver esse sistema de equações?



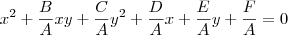
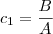 ,
, 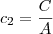 ,
, 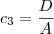 ,
, 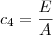 e
e 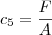 . A equação pode então ser escrita como:
. A equação pode então ser escrita como: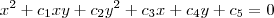



 , avisa que eu resolvo.
, avisa que eu resolvo.

