 por -civil- » Qua Ago 10, 2011 22:41
por -civil- » Qua Ago 10, 2011 22:41
Boulos - 3 ª ed. - Cap. 18
18-17) Considere as retas r: X= (1,1,0) +  (0,1,1) e s: (x-1)/2 = y = z. Sejam A o ponto de intersecção de s com o plano
(0,1,1) e s: (x-1)/2 = y = z. Sejam A o ponto de intersecção de s com o plano  , e B e C, respectivamente, os pontos em que r intercepta Oxz e O xy. Calule a área do triângulo ABC (SO), nos casos:
, e B e C, respectivamente, os pontos em que r intercepta Oxz e O xy. Calule a área do triângulo ABC (SO), nos casos:
(a)  : x - y + z = 2
: x - y + z = 2Fazendo a intersecção de s e

, encontrei o ponto A = (2,

,

)
Fazendo a intersecção entre r e Oxz
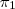
: X = (0,0,0) +

(1,0,0) +

(0,01)
1 =

1 +

= 0

=


= -1,

= -1,

= 1
B = (1, 0, -1)
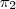
: X = (0,0,0) +

(1,0,0) +

(0,1,0)
1 =

1 +

= 0

= 0
C = (1,1,0)
Usando os três pontos para calcular o determinante, cheguei que o determinante é igual a 2 e a área será 1. Mas o resultado do livro é
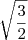
. O que tem de errado na minha resolução.
-
-civil-
- Usuário Dedicado

-
- Mensagens: 47
- Registrado em: Sex Abr 22, 2011 12:31
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Civil
- Andamento: cursando
 por LuizAquino » Sex Ago 12, 2011 13:05
por LuizAquino » Sex Ago 12, 2011 13:05
Note que:
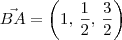
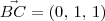
Desse modo,
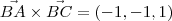
.
Para cacular a área de ABC basta tomar
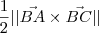
.
-civil- escreveu:Mas o resultado do livro é
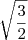
. O que tem de errado na minha resolução.
Na verdade, o resultado é
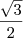
.
-

LuizAquino
- Colaborador Moderador - Professor

-
- Mensagens: 2654
- Registrado em: Sex Jan 21, 2011 09:11
- Localização: Teófilo Otoni - MG
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Mestrado - Modelagem Computacional
- Andamento: formado
-
Voltar para Geometria Analítica
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [Razão da área do triângulo para a área do quadrilátero]
 por Mayra Luna » Sex Nov 23, 2012 20:17
por Mayra Luna » Sex Nov 23, 2012 20:17
- 2 Respostas
- 4419 Exibições
- Última mensagem por Mayra Luna

Ter Nov 27, 2012 14:53
Geometria Plana
-
- [Área] Área de triangulo e trapézio
 por smlspirit » Qui Jul 19, 2012 20:07
por smlspirit » Qui Jul 19, 2012 20:07
- 1 Respostas
- 2996 Exibições
- Última mensagem por e8group

Qui Jul 19, 2012 20:57
Geometria Plana
-
- Área do Triângulo
por Padoan » Qui Fev 11, 2010 18:36
- 6 Respostas
- 8379 Exibições
- Última mensagem por MarceloFantini

Sex Fev 12, 2010 13:42
Geometria Plana
-
- Área do Triângulo
por Cleyson007 » Sex Mai 14, 2010 13:07
- 1 Respostas
- 2327 Exibições
- Última mensagem por Douglasm

Sex Mai 14, 2010 13:38
Geometria Analítica
-
- Área do Triângulo
por valeuleo » Ter Abr 05, 2011 11:25
- 1 Respostas
- 2692 Exibições
- Última mensagem por LuizAquino

Ter Abr 05, 2011 11:42
Geometria Analítica
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
função demanda
Autor:
ssousa3 - Dom Abr 03, 2011 20:55
alguém poderia me ajudar nesse exercício aqui Uma loja de CDs adquire cada unidade por R$20,00 e a revende por R$30,00. Nestas condições,
a quantidade mensal que consegue vender é 500 unidades. O proprietário estima que, reduzindo o preço para R$28,00, conseguirá vender 600 unidades por mês.
a) Obtenha a função demanda, supondo ser linear
Eu faço ensino médio mas compro apostilas de concursos para me preparar para mercado de trabalho e estudar sozinho não é fácil. Se alguém puder me ajudar aqui fico grato
Assunto:
função demanda
Autor:
ssousa3 - Seg Abr 04, 2011 14:30
Gente alguém por favor me ensine a calcular a fórmula da função demanda

Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
 (0,1,1) e s: (x-1)/2 = y = z. Sejam A o ponto de intersecção de s com o plano
(0,1,1) e s: (x-1)/2 = y = z. Sejam A o ponto de intersecção de s com o plano  , e B e C, respectivamente, os pontos em que r intercepta Oxz e O xy. Calule a área do triângulo ABC (SO), nos casos:
, e B e C, respectivamente, os pontos em que r intercepta Oxz e O xy. Calule a área do triângulo ABC (SO), nos casos: : x - y + z = 2
: x - y + z = 2 , encontrei o ponto A = (2,
, encontrei o ponto A = (2,  ,
,  )
)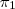 : X = (0,0,0) +
: X = (0,0,0) +  (1,0,0) +
(1,0,0) +  (0,01)
(0,01)
 = 0
= 0 =
= 
 = -1,
= -1,  = -1,
= -1,  = 1
= 1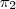 : X = (0,0,0) +
: X = (0,0,0) +  (1,0,0) +
(1,0,0) +  (0,1,0)
(0,1,0)
 = 0
= 0 = 0
= 0 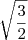 . O que tem de errado na minha resolução.
. O que tem de errado na minha resolução.

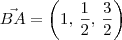
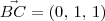
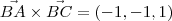 .
.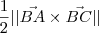 .
.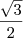 .
.
