 por stanley tiago » Sáb Fev 19, 2011 10:26
por stanley tiago » Sáb Fev 19, 2011 10:26
O cateto
b, de um trinagulo retangulo ABC , mede 12 cm e a projeçao do cateto
c sobre a hipotenusa
a vale 6 cm . calcule
a,c,h e m.eu tetei fazer assim !
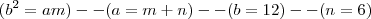
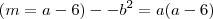


![\Delta=\sqrt[]{612} \Delta=\sqrt[]{612}](/latexrender/pictures/81bb000a195a3c359c112dbf75909f5b.png)
![\Delta=6\sqrt[]{17} \Delta=6\sqrt[]{17}](/latexrender/pictures/1d8fe4c63b7caafbca6667dde3783b0d.png)
![a'=\frac{6+6\sqrt[]{17} }{2}------a'=3+3\sqrt[]{17} a'=\frac{6+6\sqrt[]{17} }{2}------a'=3+3\sqrt[]{17}](/latexrender/pictures/d0bb369f6ebba3fe17c0bf287e6dd09f.png)
![a" =\frac{6-6\sqrt[]{17} }{2}------a" =3-3\sqrt[]{17} a" =\frac{6-6\sqrt[]{17} }{2}------a" =3-3\sqrt[]{17}](/latexrender/pictures/33a8a1fbfebf867a63db7ac7eb1dce86.png)
que nao é a resposta correta !!
agradeço deste já
-
stanley tiago
- Usuário Parceiro

-
- Mensagens: 57
- Registrado em: Seg Jan 17, 2011 14:23
- Formação Escolar: ENSINO MÉDIO
- Andamento: cursando
 por stanley tiago » Dom Fev 20, 2011 17:48
por stanley tiago » Dom Fev 20, 2011 17:48
por favor será q alguem pode me responder essa questão

-
stanley tiago
- Usuário Parceiro

-
- Mensagens: 57
- Registrado em: Seg Jan 17, 2011 14:23
- Formação Escolar: ENSINO MÉDIO
- Andamento: cursando
Voltar para Geometria Analítica
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- teorema de pitagoras
por stanley tiago » Sex Jan 21, 2011 15:59
- 5 Respostas
- 4671 Exibições
- Última mensagem por stanley tiago

Sáb Jan 22, 2011 15:49
Geometria Analítica
-
- teorema de pitagoras
por stanley tiago » Dom Fev 13, 2011 18:35
- 4 Respostas
- 3521 Exibições
- Última mensagem por stanley tiago

Seg Fev 14, 2011 22:00
Geometria Analítica
-
- Teorema de Pitágoras
por Lorrane12 » Sex Mar 23, 2012 19:50
- 9 Respostas
- 12650 Exibições
- Última mensagem por DanielFerreira

Sex Mar 30, 2012 00:19
Trigonometria
-
- Teorema de Pitágoras
por Luciana Dias » Sex Mar 23, 2012 22:46
- 2 Respostas
- 2000 Exibições
- Última mensagem por Luciana Dias

Sex Mar 23, 2012 23:06
Trigonometria
-
- [teorema de Pitágoras]
por Alane » Qui Ago 02, 2012 09:45
- 3 Respostas
- 2994 Exibições
- Última mensagem por Alane

Qui Ago 02, 2012 11:39
Geometria Espacial
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
Exercicios de polinomios
Autor:
shaft - Qua Jun 30, 2010 17:30

Então, o exercicio pede para encontrar

.
Bom, tentei resolver a questão acima desenvolvendo as duas partes em ( )...Logo dps cheguei em um resultado q nao soube o q fazer mais.
Se vcs puderem ajudar !
Assunto:
Exercicios de polinomios
Autor:
Douglasm - Qua Jun 30, 2010 17:53
Bom, se desenvolvermos isso, encontramos:

Para que os polinômios sejam iguais, seus respectivos coeficientes devem ser iguais (ax = bx ; ax² = bx², etc.):


Somando a primeira e a segunda equação:

Finalmente:

Até a próxima.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
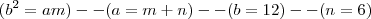
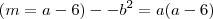


![\Delta=\sqrt[]{612} \Delta=\sqrt[]{612}](/latexrender/pictures/81bb000a195a3c359c112dbf75909f5b.png)
![\Delta=6\sqrt[]{17} \Delta=6\sqrt[]{17}](/latexrender/pictures/1d8fe4c63b7caafbca6667dde3783b0d.png)
![a'=\frac{6+6\sqrt[]{17} }{2}------a'=3+3\sqrt[]{17} a'=\frac{6+6\sqrt[]{17} }{2}------a'=3+3\sqrt[]{17}](/latexrender/pictures/d0bb369f6ebba3fe17c0bf287e6dd09f.png)
![a" =\frac{6-6\sqrt[]{17} }{2}------a" =3-3\sqrt[]{17} a" =\frac{6-6\sqrt[]{17} }{2}------a" =3-3\sqrt[]{17}](/latexrender/pictures/33a8a1fbfebf867a63db7ac7eb1dce86.png)

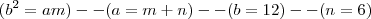
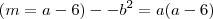


![\Delta=\sqrt[]{612} \Delta=\sqrt[]{612}](/latexrender/pictures/81bb000a195a3c359c112dbf75909f5b.png)
![\Delta=6\sqrt[]{17} \Delta=6\sqrt[]{17}](/latexrender/pictures/1d8fe4c63b7caafbca6667dde3783b0d.png)
![a'=\frac{6+6\sqrt[]{17} }{2}------a'=3+3\sqrt[]{17} a'=\frac{6+6\sqrt[]{17} }{2}------a'=3+3\sqrt[]{17}](/latexrender/pictures/d0bb369f6ebba3fe17c0bf287e6dd09f.png)
![a" =\frac{6-6\sqrt[]{17} }{2}------a" =3-3\sqrt[]{17} a" =\frac{6-6\sqrt[]{17} }{2}------a" =3-3\sqrt[]{17}](/latexrender/pictures/33a8a1fbfebf867a63db7ac7eb1dce86.png)



 .
.



