 por spyderkill » Qua Mai 09, 2012 17:31
por spyderkill » Qua Mai 09, 2012 17:31
tenho a equação f(x)=x³-2x+1 e preciso encontrar suas raizes.
como faço?
-
spyderkill
- Novo Usuário

-
- Mensagens: 1
- Registrado em: Qua Mai 09, 2012 17:28
- Formação Escolar: GRADUAÇÃO
- Área/Curso: engenharia
- Andamento: cursando
 por LuizAquino » Qua Mai 09, 2012 18:32
por LuizAquino » Qua Mai 09, 2012 18:32
spyderkill escreveu:tenho a equação f(x)=x³-2x+1 e preciso encontrar suas raizes.
como faço?
Em primeiro lugar, note que isso não é uma
equação, mas sim uma
função.
Uma
equação seria, por exemplo, dada por
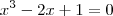
. Nesse caso, essa seria uma equação polinomial do 3° grau. Para achar as suas raízes, comece aplicando o
Teorema das Raízes Racionais para verificar se há alguma raiz racional.
-

LuizAquino
- Colaborador Moderador - Professor

-
- Mensagens: 2654
- Registrado em: Sex Jan 21, 2011 09:11
- Localização: Teófilo Otoni - MG
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Mestrado - Modelagem Computacional
- Andamento: formado
-
 por pedroaugustox47 » Sex Mai 11, 2012 02:33
por pedroaugustox47 » Sex Mai 11, 2012 02:33

nota-se que a soma dos coeficientes é 0, logo
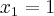
se 1 é raiz da equação, então a equação é divisível por

dividindo
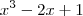
por

temos:
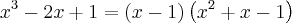

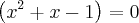
resolvendo por Báskhara temos :
![{x}_{2}=\frac{1+\sqrt[2]{5}}{2} {x}_{2}=\frac{1+\sqrt[2]{5}}{2}](/latexrender/pictures/4ebd4cfe7a308c867f65f2645953d218.png)
e
![{x}_{3}=\frac{1-\sqrt[2]{5}}{2} {x}_{3}=\frac{1-\sqrt[2]{5}}{2}](/latexrender/pictures/ef5fcd113f7df7a92fb26c0858b55cf2.png)
Qual o gabarito?
-
pedroaugustox47
- Novo Usuário

-
- Mensagens: 8
- Registrado em: Sex Mai 11, 2012 01:53
- Formação Escolar: ENSINO MÉDIO
- Área/Curso: Sistema Elite de Ensino-CN/EPCAR
- Andamento: cursando
Voltar para Polinômios
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [raízes de números complexos] Raízes de uma equação com grau
por karenfreitas » Seg Ago 22, 2016 19:08
- 1 Respostas
- 8121 Exibições
- Última mensagem por adauto martins

Sáb Ago 27, 2016 16:11
Números Complexos
-
- Raizes de equação de grau>=3
por citadp » Qua Jun 20, 2012 09:32
- 3 Respostas
- 2292 Exibições
- Última mensagem por Russman

Sex Jul 06, 2012 15:49
Cálculo: Limites, Derivadas e Integrais
-
- Raizes da equaçao do 2° grau
por hissamo » Sex Abr 10, 2015 15:57
- 1 Respostas
- 1837 Exibições
- Última mensagem por DanielFerreira

Sáb Abr 11, 2015 17:14
Equações
-
- Raizes de uma equação de terceiro grau.
por 380625 » Dom Mar 27, 2011 13:58
- 3 Respostas
- 3021 Exibições
- Última mensagem por MarceloFantini

Dom Mar 27, 2011 18:09
Funções
-
- equação de segundo grau( descobrindo as raizes)
por arturmedeiros2010 » Qui Fev 13, 2014 15:34
- 1 Respostas
- 1365 Exibições
- Última mensagem por Russman

Sex Fev 14, 2014 00:15
Equações
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
dúvida em uma questão em regra de 3!
Autor:
leandro moraes - Qui Jul 01, 2010 12:41
pessoal eu achei como resultado 180 toneladas,entretanto sei que a questão está erra pela lógica e a resposta correta segundo o gabarito é 1.800 toneladas.
me explique onde eu estou pecando na questão. resolva explicando.
78 – ( CEFET – 1993 ) Os desabamentos, em sua maioria, são causados por grande acúmulo de lixo nas encostas dos morros. Se 10 pessoas retiram 135 toneladas de lixo em 9 dias, quantas toneladas serão retiradas por 40 pessoas em 30 dias ?
Assunto:
dúvida em uma questão em regra de 3!
Autor:
Douglasm - Qui Jul 01, 2010 13:16
Observe o raciocínio:
10 pessoas - 9 dias - 135 toneladas
1 pessoa - 9 dias - 13,5 toneladas
1 pessoa - 1 dia - 1,5 toneladas
40 pessoas - 1 dia - 60 toneladas
40 pessoas - 30 dias - 1800 toneladas
Assunto:
dúvida em uma questão em regra de 3!
Autor:
leandro moraes - Qui Jul 01, 2010 13:18
pessoal já achei a resposta. o meu erro foi bobo rsrsrrs errei em uma continha de multiplicação, é mole rsrsrsr mas felizmente consegui.
Assunto:
dúvida em uma questão em regra de 3!
Autor:
leandro moraes - Qui Jul 01, 2010 13:21
leandro moraes escreveu:pessoal já achei a resposta. o meu erro foi bobo rsrsrrs errei em uma continha de multiplicação, é mole rsrsrsr mas felizmente consegui.
valeu meu camarada.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.



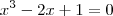 . Nesse caso, essa seria uma equação polinomial do 3° grau. Para achar as suas raízes, comece aplicando o Teorema das Raízes Racionais para verificar se há alguma raiz racional.
. Nesse caso, essa seria uma equação polinomial do 3° grau. Para achar as suas raízes, comece aplicando o Teorema das Raízes Racionais para verificar se há alguma raiz racional.

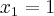

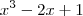 por
por  temos:
temos: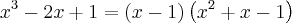

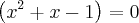
![{x}_{2}=\frac{1+\sqrt[2]{5}}{2} {x}_{2}=\frac{1+\sqrt[2]{5}}{2}](/latexrender/pictures/4ebd4cfe7a308c867f65f2645953d218.png) e
e ![{x}_{3}=\frac{1-\sqrt[2]{5}}{2} {x}_{3}=\frac{1-\sqrt[2]{5}}{2}](/latexrender/pictures/ef5fcd113f7df7a92fb26c0858b55cf2.png)
