primeiramente vamos estimar o intervalo das raizes,nao o fiz na questao anterior para mostrar como é o processo de encontrar raizes racionais,que sao tambem raizes reais,pois os racionais estao contidos nos reais e etc...
vamos usar,como fiz do exerc. do ITA,usar

logo nosso intervalo é menor que o estimado anteriormente...ficaria agora com,para raizes racionais
[-6,-4,-3,-2,-1,-4/3,-2/3,...,2,3,4,6] o qual nao mudaria muito do anterior...vamos tomar o polinomio

vamos usar a "regra de descartes" para variaçao de sinais dos coeficientes
(+,-,-,+,+) nao nos daria 2 trocas,ou seja duuas raizes reais positivas,ou nenhuma.como ja calculamos que para x=1,tem-se p(x)=0,logo teremos mais uma raiz positiva...
agora vamos estimar para raizes reais negativas

2 trocas,o qual nos da 2 raizes reais negativas ou nenhuma...
vamos agora estimar se ha raizes complexo-conjugados
tomamos o polinomio novamente

observar-se que
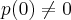 e que nao ha nenhum coeficiente nulo...
e que nao ha nenhum coeficiente nulo...temos que

como tambem temos
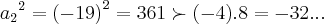

como em nenhum desses encontramos a condiçao de
p/algum k,

entao nao temos raiz complexo-conjugado,pois se encontrassemos pelo um k,que satisfaz a condiçao da "regra de huat",
mesmo tendo outros que nao satisfaça tal criterio,
teriamos raizes complexos-conjugados.



 vamos pegar mais um "gancho" na questao anterior da ENE-1950 e modificarmos o polinomio para que possamos ter raizes complexo-conjugado e encontrar a possivel localidade de suas raizes.vamos calcular o "anel",diferença entre cota-superior(disco maior) e cota inferior(disco menor).modificando o polinomio é claro que suas raizes reais serao outras,mas nosso foco serao apenas as raizes complexo-conjugado.
vamos pegar mais um "gancho" na questao anterior da ENE-1950 e modificarmos o polinomio para que possamos ter raizes complexo-conjugado e encontrar a possivel localidade de suas raizes.vamos calcular o "anel",diferença entre cota-superior(disco maior) e cota inferior(disco menor).modificando o polinomio é claro que suas raizes reais serao outras,mas nosso foco serao apenas as raizes complexo-conjugado.![\left|z \right|\preceq 1+\sqrt[r]{\left|max.({a}_{n},...,{a}_{o})/{a}_{n} \right|} \left|z \right|\preceq 1+\sqrt[r]{\left|max.({a}_{n},...,{a}_{o})/{a}_{n} \right|}](/latexrender/pictures/77c77b019a06b99d1f1a5e75c76e67e4.png)
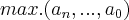

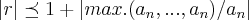
![\left|z \right|\geq 1/(1+\sqrt[r]{\left|max.({a}_{n},...,{a}_{n})/{a}_{n} \right|}) \left|z \right|\geq 1/(1+\sqrt[r]{\left|max.({a}_{n},...,{a}_{n})/{a}_{n} \right|})](/latexrender/pictures/0e7ec76a30c378ca9e92dd9bedc067cc.png)
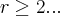
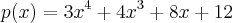

 \right|=1+4=5
\Rightarrow \left|z \right|\preceq 5... \left|z \right|\preceq 1+\left|\sqrt[4-3]({12}/3) \right|=1+4=5
\Rightarrow \left|z \right|\preceq 5...](/latexrender/pictures/3a5bfb720b1d099f3e49845e3694f6be.png)
![\left|z \right|\geq 1/(1+\sqrt[2]{12/3} \right|})=1/(1+4)=1/\sqrt[]5
\left|z \right|\geq 1/\sqrt[]5 \left|z \right|\geq 1/(1+\sqrt[2]{12/3} \right|})=1/(1+4)=1/\sqrt[]5
\left|z \right|\geq 1/\sqrt[]5](/latexrender/pictures/0f29899cb03e99cdf441a028dd642a5d.png)

![\left|{c}_{(inf)} \right|\geq 1/\sqrt[]{5}\Rightarrow -\left|{c}_{(inf)} \right|\preceq -(1/\sqrt[]{5})
\left|{c}_{(sup)} \right|-\left|{c}_{(inf)} \right|\preceq 5-(1/\sqrt[]{5}) \left|{c}_{(inf)} \right|\geq 1/\sqrt[]{5}\Rightarrow -\left|{c}_{(inf)} \right|\preceq -(1/\sqrt[]{5})
\left|{c}_{(sup)} \right|-\left|{c}_{(inf)} \right|\preceq 5-(1/\sqrt[]{5})](/latexrender/pictures/00fb6e31e812b406213fa66b85d5635d.png)
![\left|z \right|\preceq 5-(1/\sqrt[]{5}) \left|z \right|\preceq 5-(1/\sqrt[]{5})](/latexrender/pictures/84ab5a5e56ad55c427f7d423d0bc028c.png)


 substitui-se
substitui-se 
 não existem zeros.Senão vejamos
não existem zeros.Senão vejamos

 .Como se pode observar o vertice está acima do eixo Ox, estando parabola virada para cima, o vertice é um mínimo absoluto.Então basta calcular a função para os valores dos extremos do intervalo.
.Como se pode observar o vertice está acima do eixo Ox, estando parabola virada para cima, o vertice é um mínimo absoluto.Então basta calcular a função para os valores dos extremos do intervalo.