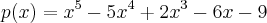
primeiramente,vamos estimar a existencia de raizes reais.calcularemos o valor de p(x) no intervalo considerado pela questao,ou seja [-10,10] e verificar se o produto
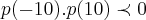
,teorema de bolzano.
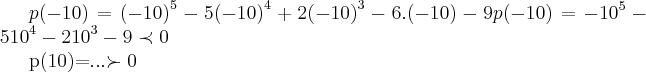
(calcule-o).logo segundo "bolzano" existe pelo menos uma raiz real no intervalo[-10,10].
vamos a "regra de descartes" da variaçao de sinais...
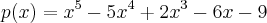
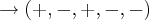
estima-se 2 raizes reais positivas ou nenhuma r.positiva
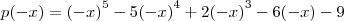
logo,estima-se 1 raiz negativa ou nenhuma raiz negativa.
agora vamos as complexos-conjugado...
pela "regra da lacuna",temos
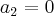
vamos tomar o produto
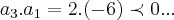
logo p(x) nao tera raizes complexo-conjugados.
podemos tambem usar "regra de hiaut-de du gua"...
tomemos
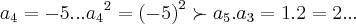



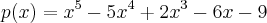
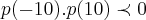 ,teorema de bolzano.
,teorema de bolzano.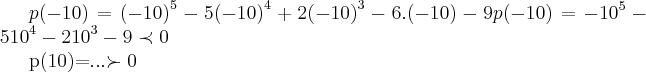
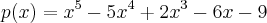
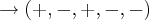
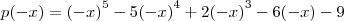
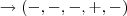
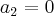
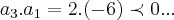
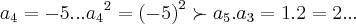

![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]} {(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]}](/latexrender/pictures/19807748a214d3361336324f3e43ea9a.png)
![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}} {(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}}](/latexrender/pictures/3d7908e5b4e397bf635b6546063d9130.png)

 , ou seja, 1 dividido por 20 é igual a 0.05 . Sendo assim, a função final é igual a vinte elevado à meio.
, ou seja, 1 dividido por 20 é igual a 0.05 . Sendo assim, a função final é igual a vinte elevado à meio. ![{0,05}^{-\frac{1}{2}} = {\frac{1}{20}}^{-\frac{1}{2}} = {\frac{20}{1}}^{\frac{1}{2}} = \sqrt[2]{20} {0,05}^{-\frac{1}{2}} = {\frac{1}{20}}^{-\frac{1}{2}} = {\frac{20}{1}}^{\frac{1}{2}} = \sqrt[2]{20}](/latexrender/pictures/c0100c6f4d8bdbb7d54165e6be7aff04.png)
 da seguinte forma:
da seguinte forma: .
. da seguinte forma:
da seguinte forma: .
.