-
-
Novo APOIA.se AjudaMatemática
por admin em Sáb Abr 25, 2020 19:01
- 0 Tópicos
- 482087 Mensagens
-
Última mensagem por admin
em Sáb Abr 25, 2020 19:01
-
-
Agradecimento aos Colaboradores
por admin em Qui Nov 15, 2018 00:25
- 0 Tópicos
- 544632 Mensagens
-
Última mensagem por admin
em Qui Nov 15, 2018 00:25
-
-
Ativação de Novos Registros
por admin em Qua Nov 14, 2018 11:58
- 0 Tópicos
- 508439 Mensagens
-
Última mensagem por admin
em Qua Nov 14, 2018 11:58
-
-
Regras do Fórum - Leia antes de postar!
por admin em Ter Mar 20, 2012 21:51
- 0 Tópicos
- 739868 Mensagens
-
Última mensagem por admin
em Ter Mar 20, 2012 21:51
-
-
DICA: Escrevendo Fórmulas com LaTeX via BBCode
por admin em Qua Ago 29, 2007 04:04
- 41 Tópicos
- 2189313 Mensagens
-
Última mensagem por Janayna
em Qui Abr 27, 2017 00:04
 por adauto martins » Sex Nov 01, 2019 11:51
por adauto martins » Sex Nov 01, 2019 11:51
vamos fazer um pequeno estudo,usando o polinomio que calculamos anteriormente do exame da ESCOLA MILITAR DO REALENGO.o estudo de polinomios é extenso,mesmo a nivel medio e um desafio sempre,pois se trata de uma equaçao diofantina nao-linear(envolve potencias de x maiores que 1(um)) e encontrar suas raizes,ou seja p(x)=0,sera sempre um desafio,e isso é que mantem a ciencia,a matematica sempre viva,sempre em abertos...
vamos indepente da restriçao do dominio da funçao original,tomar o polinomio:
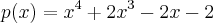
encontramos,de uma maneira suscinta,o intervalo de localizaçao das raizes(e tem diversos metodos para tal,e todos eficientes;um dos metodos mais eficiente é o de LAGUERRE,o qual vc usa p(x) e p(-x) e encontra as cotas superiores e inferiores...).no nosso caso achamos o intervalo[-3,3],para efeito de calculo rapido.
usaremos agora o teorema de bolzano(estude ai...),calculando:
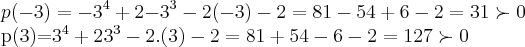
logo
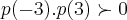
pelo teorema de bolzano,teremos um numero par de raizes reais,ou nenhuma...
se o produto
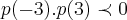
teriamos um numero impar de raizes.
agora usaremos o criterio de DESCARTES, das trocas de sinas de p(x) e p(-x)
em p(x) temos (+,+,-,-) uma troca,ou seja a possibilidade de termos uma raiz real positiva...
em p(-x) temos (+,-,+,-) duas trocas,ou seja a possiblidade de termos duas raizes negativas...
como ja mostramos que
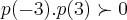
e teremos nunhuma ou um numero par de raizes.temos a seguite configuraçao:
podemos ter uma raiz positiva,uma raiz negativa ou duas raizes negativas e nenhuma positiva,pois como o polinomio é de quarto grau,podemos ter um par de raizes
complexos-conjugado.pois nao existe uma so raiz complexa,e sim em pares de
complexos-conjugados.um criterio para saber se ha raizes complexas é da pela "regra da lacuna" e 'regra de huat",que em suma diz:
se
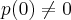
e se tomarmos algum
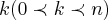
tivermos
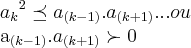
voltando ao nosso polinomio,teremos
![p(0)=-2\neq 0...
tomemos [tex]k=3...{{a}_{3}}^{2}={2}^{2}=4\succ ({a}_{4}.{a}_{2})=1.0=0 p(0)=-2\neq 0...
tomemos [tex]k=3...{{a}_{3}}^{2}={2}^{2}=4\succ ({a}_{4}.{a}_{2})=1.0=0](/latexrender/pictures/cab2f11dcba811cab63beaf947688dd9.png)
ou
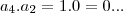
,ou seja nao temos um par de
complexos-conjugados.
logo,poderemos ter ,pelo que frizamos ate o momento uma raiz real positiva e uma raiz real negativa,ou duas raizes negativas,ou nenhuma raiz...
encontra-las,se houver, faremos adiante,no momento eu queria fazer apenas essa pequena explanaçao...
-
adauto martins
- Colaborador Voluntário

-
- Mensagens: 1171
- Registrado em: Sex Set 05, 2014 19:37
- Formação Escolar: EJA
- Área/Curso: matematica
- Andamento: cursando
 por adauto martins » Sex Nov 01, 2019 22:10
por adauto martins » Sex Nov 01, 2019 22:10
correçao:
a "regra da lacuna",postei errado:
a regra diz:
se
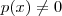
e para algum
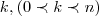
tivermos
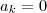
e
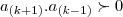
,
entao
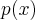
tera raizes complexas-conjugado.
e ainda se houver dois ou mais coeficientes consecutivos nulos,entao p(x) tera raizes
complexos-conjugado.
as raizes calcularei pelo metodos das tangentes,metodo de newton-raphson...mais adiante...
por agora cansei um pouco de matematica...
ps-esse exercicio que é da ESCOLA MILITAR DO REALENGO(atual AMAN),do concurso á admissao a tal escola é de 1934,ou seja em 1933 cobravam para essas escolas superiores calculo,pensa.e calculo de qualidade,equiparado aos melhores cursos de calculo 1,de nossas melhores universiodades federais atual...mudou muito...
-
adauto martins
- Colaborador Voluntário

-
- Mensagens: 1171
- Registrado em: Sex Set 05, 2014 19:37
- Formação Escolar: EJA
- Área/Curso: matematica
- Andamento: cursando
Voltar para Polinômios
Usuários navegando neste fórum: Nenhum usuário registrado e 4 visitantes
Assunto:
método de contagem
Autor:
sinuca147 - Seg Mai 25, 2009 09:10
Veja este exercício:
Se A = {

} e B = {

}, então o número de elementos A

B é:
Eu tentei resolver este exercício e achei a resposta "três", mas surgiram muitas dúvidas aqui durante a resolução.
Para determinar os elementos do conjunto A, eu tive de basicamente fazer um lista de vinte dividido por todos os números naturais maiores que zero e menores que vinte e um, finalmente identificando como elementos do conjunto A os números 1, 2, 4, 5, 10 e 20. Acho que procedi de maneira correta, mas fiquei pensando aqui se não existiria um método mais "sofisticado" e prático para que eu pudesse identificar ou ao menos contar o número de elementos do conjunto A, existe?
No processo de determinação dos elementos do conjunto B o que achei foi basicamente os múltiplos de cinco e seus opostos, daí me surgiram estas dúvidas:
existe oposto de zero?
existe inverso de zero?
zero é par, certo?
sendo x um número natural, -x é múltiplo de x?
sendo z um número inteiro negativo, z é múltiplo de z?
sendo z um número inteiro negativo, -z é múltiplo de z?
A resposta é 3?
Obrigado.
Assunto:
método de contagem
Autor:
Molina - Seg Mai 25, 2009 20:42
Boa noite, sinuca.
Se A = {

} você concorda que n só pode ser de 1 a 20? Já que pertence aos naturais?
Ou seja, quais são os divisores de 20? Eles são seis: 1, 2, 4, 5, 10 e 20.
Logo, o conjunto A é
A = {1, 2, 4, 5, 10, 20}
Se B = {

} você concorda que x será os múltiplos de 5 (positivos e negativos)? Já que m pertence ao conjunto Z?
Logo, o conjunto B é
B = {... , -25, -20, -15, -10, -5, 0, 5, 10, 15, 20, 25, ...
Feito isso precisamos ver os números que está em ambos os conjuntos, que são:
5, 10 e 20 (3 valores, como você achou).
Vou responder rapidamente suas dúvidas porque meu tempo está estourando. Qualquer dúvida, coloque aqui, ok?
sinuca147 escreveu:No processo de determinação dos elementos do conjunto B o que achei foi basicamente os múltiplos de cinco e seus opostos, daí me surgiram estas dúvidas:
existe oposto de zero? sim, é o próprio zero
existe inverso de zero? não, pois não há nenhum número que multiplicado por zero resulte em 1
zero é par, certo? sim, pois pode ser escrito da forma de 2n, onde n pertence aos inteiros
sendo x um número natural, -x é múltiplo de x? Sim, pois basta pegar x e multiplicar por -1 que encontramos -x
sendo z um número inteiro negativo, z é múltiplo de z? Sim, tais perguntando se todo número é multiplo de si mesmo
sendo z um número inteiro negativo, -z é múltiplo de z? Sim, pois basta pegar -z e multiplicar por -1 que encontramos x
A resposta é 3? Sim, pelo menos foi o que vimos a cima
Bom estudo,

Assunto:
método de contagem
Autor:
sinuca147 - Seg Mai 25, 2009 23:35
Obrigado, mas olha só este link
http://www.colegioweb.com.br/matematica ... ro-natural
neste link encontra-se a a frase:
Múltiplo de um número natural é qualquer número que possa ser obtido multiplicando o número natural por 0, 1, 2, 3, 4, 5, etc.
Para determinarmos os múltiplos de 15, por exemplo, devemos multiplicá-lo pela sucessão dos números naturais:
Ou seja, de acordo com este link -5 não poderia ser múltiplo de 5, assim como 5 não poderia ser múltiplo de -5, eu sempre achei que não interessava o sinal na questão dos múltiplos, assim como você me confirmou, mas e essa informação contrária deste site, tem alguma credibilidade?
Há e claro, a coisa mais bacana você esqueceu, quero saber se existe algum método de contagem diferente do manual neste caso:
Para determinar os elementos do conjunto A, eu tive de basicamente fazer um lista de vinte dividido por todos os números naturais maiores que zero e menores que vinte e um, finalmente identificando como elementos do conjunto A os números 1, 2, 4, 5, 10 e 20. Acho que procedi de maneira correta, mas fiquei pensando aqui se não existiria um método mais "sofisticado" e prático para que eu pudesse identificar ou ao menos contar o número de elementos do conjunto A, existe?
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
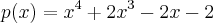
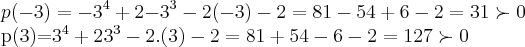
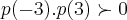
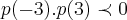
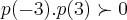 e teremos nunhuma ou um numero par de raizes.temos a seguite configuraçao:
e teremos nunhuma ou um numero par de raizes.temos a seguite configuraçao: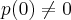 e se tomarmos algum
e se tomarmos algum 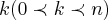
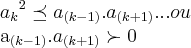
![p(0)=-2\neq 0...
tomemos [tex]k=3...{{a}_{3}}^{2}={2}^{2}=4\succ ({a}_{4}.{a}_{2})=1.0=0 p(0)=-2\neq 0...
tomemos [tex]k=3...{{a}_{3}}^{2}={2}^{2}=4\succ ({a}_{4}.{a}_{2})=1.0=0](/latexrender/pictures/cab2f11dcba811cab63beaf947688dd9.png)
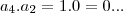 ,ou seja nao temos um par de complexos-conjugados.
,ou seja nao temos um par de complexos-conjugados.

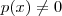 e para algum
e para algum 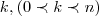
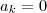 e
e 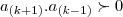 ,
, 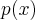
 } e B = {
} e B = { }, então o número de elementos A
}, então o número de elementos A  B é:
B é: