Sejam

,
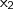
e
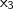
as raízes da equação em questão. De acordo com o enunciado, o produto de duas delas vale UM. Em símbolos,
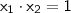
Por
Girard, temos que o produto das (três) raízes vale...
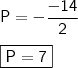
Portanto,
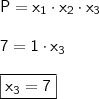
Isto é, SETE é uma raiz da equação. Dito isto, pelo
método da chave, podemos determinar a equação (de grau dois) que permitirá encontrar as demais raízes. Segue,
+ 2x³ - 19x² + 37x - 14 | x - 7
____________________| 2x² - 5x + 2
+ 2x³ - 19x²
- 2x³ + 14x²
____________________|
- 5x² + 37x - 14
+ 5x² - 35x
____________________|
+ 2x - 14
- 2x + 14
____________________|
0
Daí,
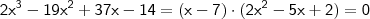
Com efeito,
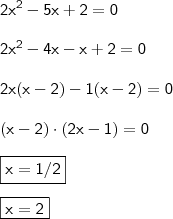
Por fim, podemos concluir que
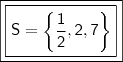
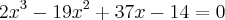 é 1. Determinar as raízes desse polinômio.
é 1. Determinar as raízes desse polinômio. 

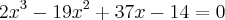 é 1. Determinar as raízes desse polinômio.
é 1. Determinar as raízes desse polinômio. 
 ,
, 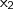 e
e 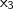 as raízes da equação em questão. De acordo com o enunciado, o produto de duas delas vale UM. Em símbolos,
as raízes da equação em questão. De acordo com o enunciado, o produto de duas delas vale UM. Em símbolos,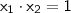
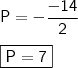
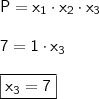
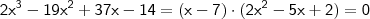
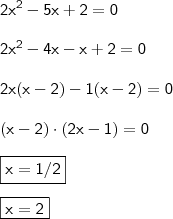
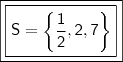


 .
.



