-
-
Novo APOIA.se AjudaMatemática
por admin em Sáb Abr 25, 2020 19:01
- 0 Tópicos
- 478816 Mensagens
-
Última mensagem por admin

em Sáb Abr 25, 2020 19:01
-
-
Agradecimento aos Colaboradores
por admin em Qui Nov 15, 2018 00:25
- 0 Tópicos
- 535807 Mensagens
-
Última mensagem por admin

em Qui Nov 15, 2018 00:25
-
-
Ativação de Novos Registros
por admin em Qua Nov 14, 2018 11:58
- 0 Tópicos
- 499447 Mensagens
-
Última mensagem por admin

em Qua Nov 14, 2018 11:58
-
-
Regras do Fórum - Leia antes de postar!
por admin em Ter Mar 20, 2012 21:51
- 0 Tópicos
- 717242 Mensagens
-
Última mensagem por admin

em Ter Mar 20, 2012 21:51
-
-
DICA: Escrevendo Fórmulas com LaTeX via BBCode
por admin em Qua Ago 29, 2007 04:04
- 41 Tópicos
- 2141819 Mensagens
-
Última mensagem por Janayna

em Qui Abr 27, 2017 00:04
 por Guga1981 » Ter Dez 13, 2016 09:24
por Guga1981 » Ter Dez 13, 2016 09:24
Olá, amigo!
Gostaria da ajuda de vocês para identificar o padrão matemático que rege o problema abaixo:
Pelo que pude entender o movimento não é uniforme. No final (no instante 7 segundos) a aceleração diminui.
Mas foi só isso que identifiquei.
Não sei por onde começar...
-
Guga1981
- Usuário Parceiro

-
- Mensagens: 53
- Registrado em: Dom Jan 18, 2015 13:27
- Localização: São Vicente-SP
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura em Matemática
- Andamento: cursando
-
 por Guga1981 » Qui Dez 15, 2016 15:21
por Guga1981 » Qui Dez 15, 2016 15:21
Joguei os dados no excel e obtive o seguinte gráfico:
- Anexos
-
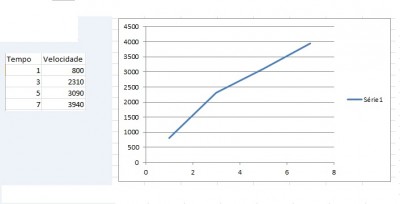
- Gráfico
-
Guga1981
- Usuário Parceiro

-
- Mensagens: 53
- Registrado em: Dom Jan 18, 2015 13:27
- Localização: São Vicente-SP
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura em Matemática
- Andamento: cursando
-
 por Guga1981 » Qui Dez 15, 2016 15:55
por Guga1981 » Qui Dez 15, 2016 15:55
Peguei os pontos (5 segundos - 3090 cm/s) e (7 segundos - 3940 cm/s) e montei a equação geral da reta (da segunda parte da reta do gráfico), através do cálculo de determinante:
- Anexos
-
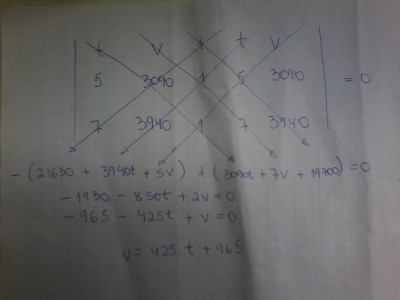
-
Guga1981
- Usuário Parceiro

-
- Mensagens: 53
- Registrado em: Dom Jan 18, 2015 13:27
- Localização: São Vicente-SP
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura em Matemática
- Andamento: cursando
-
 por Guga1981 » Qui Dez 15, 2016 15:59
por Guga1981 » Qui Dez 15, 2016 15:59
mas, quando preenchi os "buracos" da primeira tabela com os tempos que faltavam (4 segundos, 6 segundos), usando a equação geral da reta, obtive outro gráfico diferente:
... o que será que está errado?...
- Anexos
-
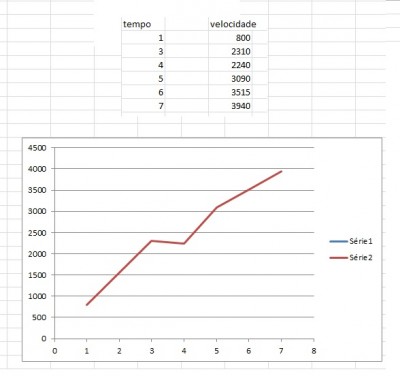
-
Guga1981
- Usuário Parceiro

-
- Mensagens: 53
- Registrado em: Dom Jan 18, 2015 13:27
- Localização: São Vicente-SP
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura em Matemática
- Andamento: cursando
-
 por adauto martins » Sex Dez 16, 2016 10:59
por adauto martins » Sex Dez 16, 2016 10:59
a queda do paraquedista é regida pela equaçao:

,onde m=massa do paraq.,k=atrito devido ao ar...colocando na forma de uma EDO, teremos:
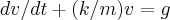
,cuja soluçao é dada por:
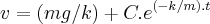
,C é devido a integraçao indefinida da EDO...usa-se os dados da tabela pra achar m,k,C...como o problema pede um polinomio,entao deve-se usar a expansao de taylor da funçao
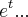
,que é dado por:

,q. em nosso caso:
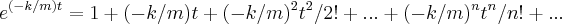
,o grau do polinomio sera dado em funçao da tabela...em se tratando de um problema de fisica classica,sera ate o segundo grau...
-
adauto martins
- Colaborador Voluntário

-
- Mensagens: 1171
- Registrado em: Sex Set 05, 2014 19:37
- Formação Escolar: EJA
- Área/Curso: matematica
- Andamento: cursando
Voltar para Polinômios
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Como posso Identificar o domínio ?
por Amanda j » Seg Out 24, 2016 12:57
- 0 Respostas
- 3340 Exibições
- Última mensagem por Amanda j

Seg Out 24, 2016 12:57
Cálculo: Limites, Derivadas e Integrais
-
- Identificar funções pares e ímpares
por vmouc » Sex Mar 11, 2011 00:17
- 6 Respostas
- 4873 Exibições
- Última mensagem por vmouc

Sex Mar 11, 2011 19:33
Funções
-
- Identificar erro na resolução, se houver
por Danilo » Seg Mar 19, 2012 22:46
- 2 Respostas
- 1642 Exibições
- Última mensagem por Juvenal

Qua Mar 21, 2012 10:08
Álgebra Elementar
-
- [Desvio Padrão] Porcentagem do desvio padrão
por GBT » Qui Mar 22, 2012 22:53
- 2 Respostas
- 13515 Exibições
- Última mensagem por fernando7

Dom Mai 13, 2018 21:55
Estatística
-
- Desvio Padrão
 por Cleyson007 » Sáb Jun 13, 2009 11:18
por Cleyson007 » Sáb Jun 13, 2009 11:18
- 1 Respostas
- 4099 Exibições
- Última mensagem por Felipe Schucman

Qua Jul 29, 2009 02:22
Estatística
Usuários navegando neste fórum: Nenhum usuário registrado e 11 visitantes
Assunto:
[Função] do primeiro grau e quadratica
Autor:
Thassya - Sáb Out 01, 2011 16:20
1) Para que os pontos (1,3) e (-3,1) pertençam ao grafico da função f(X)=ax + b ,o valor de b-a deve ser ?
2)Qual o maior valor assumido pela função f : [-7 ,10] em R definida por f(x) = x ao quadrado - 5x + 9?
3) A função f, do primeiro grau, é definida pos f(x)= 3x + k para que o gráfico de f corte o eixo das ordenadas no ponto de ordenada 5 é?
Assunto:
[Função] do primeiro grau e quadratica
Autor:
Neperiano - Sáb Out 01, 2011 19:46
Ola
Qual as suas dúvidas?
O que você não está conseguindo fazer?
Nos mostre para podermos ajudar
Atenciosamente
Assunto:
[Função] do primeiro grau e quadratica
Autor:
joaofonseca - Sáb Out 01, 2011 20:15
1)Dados dois pontos A=(1,3) e B=(-3,1) de uma reta, é possivel definir a sua equação.


Em

substitui-se
m, substitui-se
y e
x por um dos pares ordenados, e resolve-se em ordem a
b.

2)Na equação

não existem zeros.Senão vejamos
Completando o quadrado,

As coordenadas do vertice da parabola são

O eixo de simetria é a reta

.Como se pode observar o vertice está acima do eixo Ox, estando parabola virada para cima, o vertice é um mínimo absoluto.Então basta calcular a função para os valores dos extremos do intervalo.
f(-7)=93
f(10)=59
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.


 ,onde m=massa do paraq.,k=atrito devido ao ar...colocando na forma de uma EDO, teremos:
,onde m=massa do paraq.,k=atrito devido ao ar...colocando na forma de uma EDO, teremos: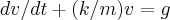 ,cuja soluçao é dada por:
,cuja soluçao é dada por: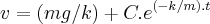 ,C é devido a integraçao indefinida da EDO...usa-se os dados da tabela pra achar m,k,C...como o problema pede um polinomio,entao deve-se usar a expansao de taylor da funçao
,C é devido a integraçao indefinida da EDO...usa-se os dados da tabela pra achar m,k,C...como o problema pede um polinomio,entao deve-se usar a expansao de taylor da funçao 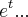 ,que é dado por:
,que é dado por: ,q. em nosso caso:
,q. em nosso caso: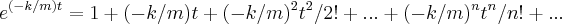 ,o grau do polinomio sera dado em funçao da tabela...em se tratando de um problema de fisica classica,sera ate o segundo grau...
,o grau do polinomio sera dado em funçao da tabela...em se tratando de um problema de fisica classica,sera ate o segundo grau...


 substitui-se
substitui-se 
 não existem zeros.Senão vejamos
não existem zeros.Senão vejamos

 .Como se pode observar o vertice está acima do eixo Ox, estando parabola virada para cima, o vertice é um mínimo absoluto.Então basta calcular a função para os valores dos extremos do intervalo.
.Como se pode observar o vertice está acima do eixo Ox, estando parabola virada para cima, o vertice é um mínimo absoluto.Então basta calcular a função para os valores dos extremos do intervalo.