 por +Danilo2 » Qui Set 29, 2016 10:43
por +Danilo2 » Qui Set 29, 2016 10:43
Como fatorar esse polinômio,

, na forma de binômio?
Bom, eu tentei escreve-lo da seguinte forma

. Como o segundo termo do binômio não gera o termo do meio do polinômio supracitado, permaneço com a dúvida.
-
+Danilo2
- Novo Usuário

-
- Mensagens: 4
- Registrado em: Qui Set 29, 2016 10:15
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura em Matemática
- Andamento: cursando
 por DanielFerreira » Sex Set 30, 2016 01:22
por DanielFerreira » Sex Set 30, 2016 01:22
Olá Danilo, seja bem-vindo!
![\\ \mathsf{x^4 + 5x^2 + 4 =} \\\\ \mathsf{x^4 + (4x^2 + x^2) + 4 =} \\\\ \mathsf{(x^4 + 4x^2) + (x^2 + 4) =} \\\\ \mathsf{x^2(x^2 + 4) + 1(x^2 + 4) =} \\\\ \mathsf{(x^2 + 4)[x^2 + 1]} = \\\\ \boxed{\mathsf{(x^2 + 4)(x^2 + 1)}} \\ \mathsf{x^4 + 5x^2 + 4 =} \\\\ \mathsf{x^4 + (4x^2 + x^2) + 4 =} \\\\ \mathsf{(x^4 + 4x^2) + (x^2 + 4) =} \\\\ \mathsf{x^2(x^2 + 4) + 1(x^2 + 4) =} \\\\ \mathsf{(x^2 + 4)[x^2 + 1]} = \\\\ \boxed{\mathsf{(x^2 + 4)(x^2 + 1)}}](/latexrender/pictures/01a1de09ebb5a44129c547fe0e0c83ae.png)
Espero ter ajudado!
A propósito, uma outra saída seria por "soma e produto" das raízes. Tome
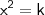
, afim de visualizar com mais clareza, e aplique o "método".
"Sabedoria é saber o que fazer;
habilidade é saber como fazer;
virtude é fazer."
(David S. Jordan)
--------------------------------------------------------------------------------
-
DanielFerreira
- Colaborador - em formação

-
- Mensagens: 1732
- Registrado em: Qui Jul 23, 2009 21:34
- Localização: Mangaratiba - RJ
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura em Matemática - IFRJ
- Andamento: formado
-
 por Soprano » Sex Set 30, 2016 13:31
por Soprano » Sex Set 30, 2016 13:31
-
Soprano
- Usuário Ativo

-
- Mensagens: 21
- Registrado em: Dom Fev 14, 2016 10:13
- Formação Escolar: ENSINO MÉDIO
- Área/Curso: Electrónica
- Andamento: cursando
 por DanielFerreira » Sáb Out 01, 2016 20:51
por DanielFerreira » Sáb Out 01, 2016 20:51
Não. Os termos entre parênteses devem ser iguais, assim poderá colocá-los em evidência!
"Sabedoria é saber o que fazer;
habilidade é saber como fazer;
virtude é fazer."
(David S. Jordan)
--------------------------------------------------------------------------------
-
DanielFerreira
- Colaborador - em formação

-
- Mensagens: 1732
- Registrado em: Qui Jul 23, 2009 21:34
- Localização: Mangaratiba - RJ
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura em Matemática - IFRJ
- Andamento: formado
-
 por Soprano » Dom Out 02, 2016 20:48
por Soprano » Dom Out 02, 2016 20:48
Não entendi, importa-se de explicar melhor? obrigado
-
Soprano
- Usuário Ativo

-
- Mensagens: 21
- Registrado em: Dom Fev 14, 2016 10:13
- Formação Escolar: ENSINO MÉDIO
- Área/Curso: Electrónica
- Andamento: cursando
 por +Danilo2 » Sáb Out 08, 2016 18:17
por +Danilo2 » Sáb Out 08, 2016 18:17
DanielFerreira escreveu: Olá Danilo. Seja bem vindo.
![\\ \mathsf{x^4 + 5x^2 + 4 =} \\\\ \mathsf{x^4 + (4x^2 + x^2) + 4 =} \\\\ \mathsf{(x^4 + 4x^2) + (x^2 + 4) =} \\\\ \mathsf{x^2(x^2 + 4) + 1(x^2 + 4) =} \\\\ \mathsf{(x^2 + 4)[x^2 + 1]} = \\\\ \boxed{\mathsf{(x^2 + 4)(x^2 + 1)}} \\ \mathsf{x^4 + 5x^2 + 4 =} \\\\ \mathsf{x^4 + (4x^2 + x^2) + 4 =} \\\\ \mathsf{(x^4 + 4x^2) + (x^2 + 4) =} \\\\ \mathsf{x^2(x^2 + 4) + 1(x^2 + 4) =} \\\\ \mathsf{(x^2 + 4)[x^2 + 1]} = \\\\ \boxed{\mathsf{(x^2 + 4)(x^2 + 1)}}](/latexrender/pictures/01a1de09ebb5a44129c547fe0e0c83ae.png)
Espero ter ajudado!
A propósito, uma outra saída seria por "soma e produto" das raízes. Tome
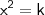
, afim de visualizar com mais clareza, e aplique o "método".
Muito obrigado pela ajuda
-
+Danilo2
- Novo Usuário

-
- Mensagens: 4
- Registrado em: Qui Set 29, 2016 10:15
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura em Matemática
- Andamento: cursando
Voltar para Polinômios
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- fatoração de Polinômio fatoração de agrupamento
por Estudante13 » Sex Nov 09, 2012 22:52
- 1 Respostas
- 3259 Exibições
- Última mensagem por Cleyson007

Sex Nov 09, 2012 23:06
Álgebra Elementar
-
- Fatoração de Polinômio
por Gobate » Dom Nov 21, 2010 01:50
- 1 Respostas
- 1921 Exibições
- Última mensagem por OtavioBonassi

Qua Jan 05, 2011 21:38
Polinômios
-
- Fatoração de Polinômio
por Jacques » Sex Set 02, 2016 22:24
- 1 Respostas
- 2319 Exibições
- Última mensagem por adauto martins

Sáb Set 10, 2016 14:41
Álgebra Elementar
-
- Fatoração e raízes de um polinômio
por pablohas » Qua Dez 08, 2010 21:26
- 2 Respostas
- 3767 Exibições
- Última mensagem por Elcioschin

Sex Dez 10, 2010 22:05
Polinômios
-
- [Equação do segundo grau]Resolvida por fatoração.
por Matheus Lacombe O » Sáb Jan 05, 2013 14:45
- 5 Respostas
- 5126 Exibições
- Última mensagem por ant_dii

Ter Jan 08, 2013 23:46
Equações
Usuários navegando neste fórum: Nenhum usuário registrado e 2 visitantes
Assunto:
cálculo de limites
Autor:
Hansegon - Seg Ago 25, 2008 11:29
Bom dia.
Preciso de ajuda na solução deste problema, pois só chego ao resultado de 0 sobre 0.
Obrigado
\lim_{x\rightarrow-1} x³ +1/x²-1[/tex]
Assunto:
cálculo de limites
Autor:
Molina - Seg Ago 25, 2008 13:25

Realmente se você jogar o -1 na equação dá 0 sobre 0.
Indeterminações deste tipo você pode resolver por L'Hôpital
que utiliza derivada.
Outro modo é transformar o numerador e/ou denominador
para que não continue dando indeterminado.
Dica: dividir o numerador e o denominador por algum valor é uma forma que normalmente dá certo.

Caso ainda não tenha dado uma

, avisa que eu resolvo.
Bom estudo!
Assunto:
cálculo de limites
Autor:
Guill - Dom Abr 08, 2012 16:03



Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
 , na forma de binômio?
, na forma de binômio? . Como o segundo termo do binômio não gera o termo do meio do polinômio supracitado, permaneço com a dúvida.
. Como o segundo termo do binômio não gera o termo do meio do polinômio supracitado, permaneço com a dúvida.
 , na forma de binômio?
, na forma de binômio? . Como o segundo termo do binômio não gera o termo do meio do polinômio supracitado, permaneço com a dúvida.
. Como o segundo termo do binômio não gera o termo do meio do polinômio supracitado, permaneço com a dúvida.
![\\ \mathsf{x^4 + 5x^2 + 4 =} \\\\ \mathsf{x^4 + (4x^2 + x^2) + 4 =} \\\\ \mathsf{(x^4 + 4x^2) + (x^2 + 4) =} \\\\ \mathsf{x^2(x^2 + 4) + 1(x^2 + 4) =} \\\\ \mathsf{(x^2 + 4)[x^2 + 1]} = \\\\ \boxed{\mathsf{(x^2 + 4)(x^2 + 1)}} \\ \mathsf{x^4 + 5x^2 + 4 =} \\\\ \mathsf{x^4 + (4x^2 + x^2) + 4 =} \\\\ \mathsf{(x^4 + 4x^2) + (x^2 + 4) =} \\\\ \mathsf{x^2(x^2 + 4) + 1(x^2 + 4) =} \\\\ \mathsf{(x^2 + 4)[x^2 + 1]} = \\\\ \boxed{\mathsf{(x^2 + 4)(x^2 + 1)}}](/latexrender/pictures/01a1de09ebb5a44129c547fe0e0c83ae.png)
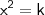 , afim de visualizar com mais clareza, e aplique o "método".
, afim de visualizar com mais clareza, e aplique o "método".
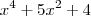

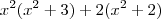
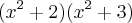



, afim de visualizar com mais clareza, e aplique o "método".



 , avisa que eu resolvo.
, avisa que eu resolvo.

