sendo p(r)=p(1/r)=0 implicar p(r+1/r)=0...
tomemos o polinomio do exercicio anterior,de 1° especie,a saber
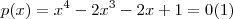
dividindo por

teremos
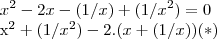
faremos
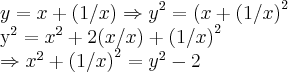
logo (*) sera
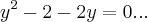
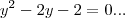
cujas raizes serao:
![{y}_{(1,2)}=(2(+,-)\sqrt[]{6})/2 {y}_{(1,2)}=(2(+,-)\sqrt[]{6})/2](/latexrender/pictures/381ff9e3b150f6d778738c4ab63c7767.png)
como
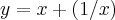
retorne as equaçoes em x,termine como exercicio...
a equaçao (1) tera raizes complexo-conjugado,pois
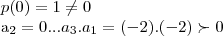
o calculo dessas raizes complexo-conjugado faremos adiante...


![{y}_{(1,2)}=(2(+,-)\sqrt[]{4-4.(-2)})/2=2(+,-)\sqrt[]{12})/2
{y}_{(1,2)}=(2(+,-)2\sqrt[]{3})/2=1(+,-)\sqrt[]{3}... {y}_{(1,2)}=(2(+,-)\sqrt[]{4-4.(-2)})/2=2(+,-)\sqrt[]{12})/2
{y}_{(1,2)}=(2(+,-)2\sqrt[]{3})/2=1(+,-)\sqrt[]{3}...](/latexrender/pictures/17e1f1e4d8392e4683998d5a77f808fb.png)
 em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto.
em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto. o ângulo entre o eixo horizontal e o afixo
o ângulo entre o eixo horizontal e o afixo  . O triângulo é retângulo com catetos
. O triângulo é retângulo com catetos  e
e  , tal que
, tal que  . Seja
. Seja  o ângulo complementar. Então
o ângulo complementar. Então  . Como
. Como  , o ângulo que o afixo
, o ângulo que o afixo  formará com a horizontal será
formará com a horizontal será  , então
, então  . Como módulo é um:
. Como módulo é um:  .
. .
.