 por adauto martins » Ter Nov 05, 2019 22:05
por adauto martins » Ter Nov 05, 2019 22:05
(ITA-instituto tecnologico de aeronautica-exame vestibular ?)
em que intervalo estao as raizes da equaçao

?
a)[-150,200] b)[-14,-12] c)[12,13] d)[-10,10] e)n.d.r
Editado pela última vez por
adauto martins em Ter Nov 05, 2019 22:38, em um total de 1 vez.
-
adauto martins
- Colaborador Voluntário

-
- Mensagens: 1171
- Registrado em: Sex Set 05, 2014 19:37
- Formação Escolar: EJA
- Área/Curso: matematica
- Andamento: cursando
 por adauto martins » Ter Nov 05, 2019 22:37
por adauto martins » Ter Nov 05, 2019 22:37
soluçao:
vamos fazer a cota inferior,ou seja:
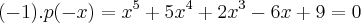
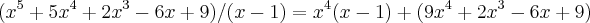
...

logo a cota inferior sera de -4,ou seja
![[-4,{c}_{s}] [-4,{c}_{s}]](/latexrender/pictures/ed0ca8cdb394eb9b31018757f3d9b1c8.png)
...deixo o calculo da cota-superior,que pelo proprio polinomio e metodo de "laguerre" e menor que 10...das alternativas apresentadas,podemos "afirmar ser a letra d)...
podemos ainda usar:
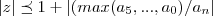
onde

é o maior dos coefiecentes em em valor positivo de p(x)...em nosso caso
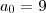
logo
![\left|z \right|\preceq 1+\left|9/1 \right|=1+9=10\Rightarrow
\left|z \right|\preceq 10\Rightarrow -10\preceq z \preceq 10
[-10,10]... \left|z \right|\preceq 1+\left|9/1 \right|=1+9=10\Rightarrow
\left|z \right|\preceq 10\Rightarrow -10\preceq z \preceq 10
[-10,10]...](/latexrender/pictures/f335078d5516bcefd94e7e06d906600e.png)
-
adauto martins
- Colaborador Voluntário

-
- Mensagens: 1171
- Registrado em: Sex Set 05, 2014 19:37
- Formação Escolar: EJA
- Área/Curso: matematica
- Andamento: cursando
Voltar para Polinômios
Usuários navegando neste fórum: Nenhum usuário registrado e 2 visitantes
Assunto:
Taxa de variação
Autor:
felipe_ad - Ter Jun 29, 2010 19:44
Como resolvo uma questao desse tipo:
Uma usina de britagem produz pó de pedra, que ao ser depositado no solo, forma uma pilha cônica onde a altura é aproximadamente igual a 4/3 do raio da base.
(a) Determinar a razão de variação do volume em relação ao raio da base.
(b) Se o raio da base varia a uma taxa de 20 cm/s, qual a razão de variação do volume quando o raio mede 2 m?
A letra (a) consegui resolver e cheguei no resultado correto de

Porem, nao consegui chegar a um resultado correto na letra (b). A resposta certa é

Alguem me ajuda? Agradeço desde já.
Assunto:
Taxa de variação
Autor:
Elcioschin - Qua Jun 30, 2010 20:47
V = (1/3)*pi*r²*h ----> h = 4r/3
V = (1/3)*pi*r²*(4r/3) ----> V = (4*pi/9)*r³
Derivando:
dV/dr = (4*pi/9)*(3r²) -----> dV/dr = 4pi*r²/3
Para dr = 20 cm/s = 0,2 m/s e R = 2 m ----> dV/0,2 = (4*pi*2²)/3 ----> dV = (3,2/3)*pi ----> dV ~= 1,066*pi m³/s
Assunto:
Taxa de variação
Autor:
Guill - Ter Fev 21, 2012 21:17
Temos que o volume é dado por:

Temos, portanto, o volume em função do raio. Podemos diferenciar implicitamente ambos os lados da equação em função do tempo, para encontrar as derivadas em função do tempo:

Sabendo que a taxa de variação do raio é 0,2 m/s e que queremos ataxa de variação do volume quando o raio for 2 m:


Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
 ?
?
 ?
?
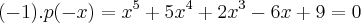
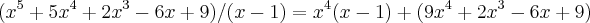

![[-4,{c}_{s}] [-4,{c}_{s}]](/latexrender/pictures/ed0ca8cdb394eb9b31018757f3d9b1c8.png) ...deixo o calculo da cota-superior,que pelo proprio polinomio e metodo de "laguerre" e menor que 10...das alternativas apresentadas,podemos "afirmar ser a letra d)...
...deixo o calculo da cota-superior,que pelo proprio polinomio e metodo de "laguerre" e menor que 10...das alternativas apresentadas,podemos "afirmar ser a letra d)...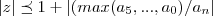

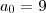
![\left|z \right|\preceq 1+\left|9/1 \right|=1+9=10\Rightarrow
\left|z \right|\preceq 10\Rightarrow -10\preceq z \preceq 10
[-10,10]... \left|z \right|\preceq 1+\left|9/1 \right|=1+9=10\Rightarrow
\left|z \right|\preceq 10\Rightarrow -10\preceq z \preceq 10
[-10,10]...](/latexrender/pictures/f335078d5516bcefd94e7e06d906600e.png)






