 por Cleyson007 » Ter Jun 02, 2009 15:36
por Cleyson007 » Ter Jun 02, 2009 15:36
Boa tarde!
Alguém pode me ajudar com a resolução do exercício abaixo?
--> Determine o polinômio P(x) de 4º grau, para o qual P(0)=72, que tem raízes duplas 2 e -3.
Estou resolvendo assim:
Como o polinômio P(x) tem raízes duplas 2 e -3 -->
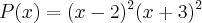
O polinômio P(x) está seguinte forma:
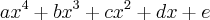
Como o enunciado diz que
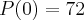
, penso que o termo independente (

) tem o valor de
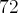
.
Como concluir o raciocínio?
Agradeço sua ajuda!
Até mais.
Um abraço.
-

Cleyson007
- Colaborador Voluntário

-
- Mensagens: 1228
- Registrado em: Qua Abr 30, 2008 00:08
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Matemática UFJF
- Andamento: formado
 por Marcampucio » Ter Jun 02, 2009 16:10
por Marcampucio » Ter Jun 02, 2009 16:10
Cleyson007 escreveu:Boa tarde!
Alguém pode me ajudar com a resolução do exercício abaixo?
--> Determine o polinômio P(x) de 4º grau, para o qual P(0)=72, que tem raízes duplas 2 e -3.
Estou resolvendo assim:
Como o polinômio P(x) tem raízes duplas 2 e -3 -->
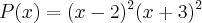
O polinômio P(x) está seguinte forma:
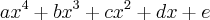
Como o enunciado diz que
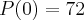
, penso que o termo independente (

) tem o valor de
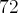
.
Como concluir o raciocínio?
Agradeço sua ajuda!
Até mais.
Um abraço.
Desenvolva
A revelação não acontece ao encontrar o sábio no alto da montanha. A revelação vem com a subida da montanha.
-
Marcampucio
- Colaborador Voluntário

-
- Mensagens: 180
- Registrado em: Ter Mar 10, 2009 17:48
- Localização: São Paulo
- Formação Escolar: GRADUAÇÃO
- Área/Curso: geologia
- Andamento: formado
 por Cleyson007 » Qua Jun 03, 2009 11:59
por Cleyson007 » Qua Jun 03, 2009 11:59
Bom dia!
A minha dúvida era no
porque do coeficiente

em:
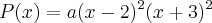
Agora entendi o raciocínio.
Obrigado pela ajuda!
Até mais
-

Cleyson007
- Colaborador Voluntário

-
- Mensagens: 1228
- Registrado em: Qua Abr 30, 2008 00:08
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Matemática UFJF
- Andamento: formado
Voltar para Polinômios
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Polinomio de grau 3
por Thassya » Dom Out 24, 2010 16:12
- 0 Respostas
- 1216 Exibições
- Última mensagem por Thassya

Dom Out 24, 2010 16:12
Polinômios
-
- Grau do polinômio em Zn[x]
por Crist » Sáb Mai 31, 2014 21:10
- 2 Respostas
- 1887 Exibições
- Última mensagem por Crist

Ter Jun 03, 2014 09:54
Álgebra Elementar
-
- Demonstração de Polinômio de 4º grau
por lucas1365 » Dom Jun 21, 2009 10:31
- 1 Respostas
- 2143 Exibições
- Última mensagem por Cleyson007

Seg Jun 22, 2009 18:20
Polinômios
-
- Raizes de um polinomio de grau 3
por Lilavet » Qua Abr 28, 2010 09:42
- 2 Respostas
- 5696 Exibições
- Última mensagem por DeMoNaZ

Qua Abr 28, 2010 18:25
Polinômios
-
- Questão - Polinômio Grau 3 - Teorema do Valor Intermediário
por elisafrombrazil » Sáb Jan 21, 2017 10:41
- 4 Respostas
- 4849 Exibições
- Última mensagem por e8group

Qui Fev 02, 2017 23:41
Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
Unesp - 95 Números Complexos
Autor:
Alucard014 - Dom Ago 01, 2010 18:22
(UNESP - 95) Seja L o Afixo de um Número complexo

em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto.
Assunto:
Unesp - 95 Números Complexos
Autor:
MarceloFantini - Qui Ago 05, 2010 17:27
Seja

o ângulo entre o eixo horizontal e o afixo

. O triângulo é retângulo com catetos

e

, tal que

. Seja

o ângulo complementar. Então

. Como

, o ângulo que o afixo

formará com a horizontal será

, mas negativo pois tem de ser no quarto quadrante. Se

, então

. Como módulo é um:

.
Logo, o afixo é

.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
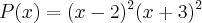
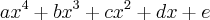
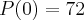 , penso que o termo independente (
, penso que o termo independente ( ) tem o valor de
) tem o valor de 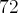 .
.


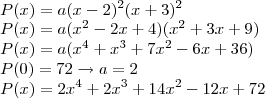
 em:
em: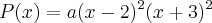
 em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto.
em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto. o ângulo entre o eixo horizontal e o afixo
o ângulo entre o eixo horizontal e o afixo  e
e  , tal que
, tal que  . Seja
. Seja  o ângulo complementar. Então
o ângulo complementar. Então  . Como
. Como  , o ângulo que o afixo
, o ângulo que o afixo  formará com a horizontal será
formará com a horizontal será  , então
, então  . Como módulo é um:
. Como módulo é um:  .
. .
.