 por fernandocez » Dom Mar 06, 2011 12:52
por fernandocez » Dom Mar 06, 2011 12:52
Caros amigos essa tá me dando trabalho. Deve ter um modo mais fácil.
47. As raízes da equação x²-7x-5 = 0 são m e n. Uma equação do segundo grau cujas raízes são
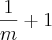
e
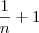
é:
resp: 5x²-3x-3=0
Eu fiz assim:
Tentei encontrar as raízes, delta = 69
x' =
![\frac{7+\sqrt[]{69}}{2} \frac{7+\sqrt[]{69}}{2}](/latexrender/pictures/a7cae91ca282913818f62f676df2f4a8.png)
x" =
![\frac{7-\sqrt[]{69}}{2} \frac{7-\sqrt[]{69}}{2}](/latexrender/pictures/6d49063d48d2a5a44132f9f164220d42.png)
substitui "m" por x'
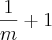
substitui "n" por x"
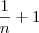
pensei que com isso encontraria as raízes da outra equação procurada, só que apareceu tanto cálculo que acho que estou no caminho errado.
-

fernandocez
- Colaborador Voluntário

-
- Mensagens: 131
- Registrado em: Seg Fev 14, 2011 15:01
- Localização: São João de Meriti - RJ
- Formação Escolar: GRADUAÇÃO
- Área/Curso: licenciatura em matemática
- Andamento: formado
 por LuizAquino » Dom Mar 06, 2011 13:09
por LuizAquino » Dom Mar 06, 2011 13:09
DicaA soma das raízes da equação original é
m + n = 7. Já o produto entre elas é
mn = -5.
A soma
s das raízes da nova equação do segundo grau será
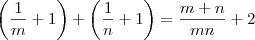
.
A produto
p das raízes da nova equação do segundo grau será
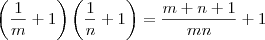
.
A nova equação do segundo grau terá o formato
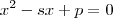
.
-

LuizAquino
- Colaborador Moderador - Professor

-
- Mensagens: 2654
- Registrado em: Sex Jan 21, 2011 09:11
- Localização: Teófilo Otoni - MG
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Mestrado - Modelagem Computacional
- Andamento: formado
-
 por fernandocez » Dom Mar 06, 2011 16:46
por fernandocez » Dom Mar 06, 2011 16:46
Valeu Luiz. Consegui resolver a partir das suas explicações, ficou muito fácil e eliminou quase todos cálculos. Só ficou uma dúvida, m+n = 7 e não -7, sempre inverto o sinal? Se fosse uma equação por exemplo: x²+5+6 o meu m+n = -5 e m.n = 6 (mantenho o sinal no produto).
-

fernandocez
- Colaborador Voluntário

-
- Mensagens: 131
- Registrado em: Seg Fev 14, 2011 15:01
- Localização: São João de Meriti - RJ
- Formação Escolar: GRADUAÇÃO
- Área/Curso: licenciatura em matemática
- Andamento: formado
 por LuizAquino » Dom Mar 06, 2011 17:46
por LuizAquino » Dom Mar 06, 2011 17:46
fernandocez escreveu:Só ficou uma dúvida, m+n = 7 e não -7, sempre inverto o sinal? Se fosse uma equação por exemplo: x²+5+6 o meu m+n = -5 e m.n = 6 (mantenho o sinal no produto).
Faça uma pesquisa sobre soma e produto das raízes de uma equação do segundo grau. Você mesmo poderá responder essas perguntas.
Comece, por exemplo, visitando a Wikipédia:
Equação quadráticahttp://pt.wikipedia.org/wiki/Equa%C3%A7 ... gundo_grau
-

LuizAquino
- Colaborador Moderador - Professor

-
- Mensagens: 2654
- Registrado em: Sex Jan 21, 2011 09:11
- Localização: Teófilo Otoni - MG
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Mestrado - Modelagem Computacional
- Andamento: formado
-
Voltar para Polinômios
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Questão prova concurso
por fernandocez » Sáb Fev 26, 2011 19:10
- 6 Respostas
- 3567 Exibições
- Última mensagem por fernandocez

Sáb Fev 26, 2011 22:29
Geometria Plana
-
- Questão prova concurso
por fernandocez » Sáb Fev 26, 2011 23:27
- 3 Respostas
- 2507 Exibições
- Última mensagem por fernandocez

Dom Fev 27, 2011 10:33
Funções
-
- Questão prova concurso (sen e cos)
por fernandocez » Qua Mar 02, 2011 11:26
- 13 Respostas
- 9301 Exibições
- Última mensagem por fernandocez

Dom Mar 13, 2011 12:18
Trigonometria
-
- Questão prova concurso com Latitude
por fernandocez » Sáb Fev 26, 2011 23:38
- 2 Respostas
- 1827 Exibições
- Última mensagem por fernandocez

Qua Mar 02, 2011 11:27
Geometria Plana
-
- Questão prova concurso combinatória
por fernandocez » Ter Mar 01, 2011 12:35
- 2 Respostas
- 2680 Exibições
- Última mensagem por fernandocez

Qui Mar 03, 2011 22:47
Estatística
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
função demanda
Autor:
ssousa3 - Dom Abr 03, 2011 20:55
alguém poderia me ajudar nesse exercício aqui Uma loja de CDs adquire cada unidade por R$20,00 e a revende por R$30,00. Nestas condições,
a quantidade mensal que consegue vender é 500 unidades. O proprietário estima que, reduzindo o preço para R$28,00, conseguirá vender 600 unidades por mês.
a) Obtenha a função demanda, supondo ser linear
Eu faço ensino médio mas compro apostilas de concursos para me preparar para mercado de trabalho e estudar sozinho não é fácil. Se alguém puder me ajudar aqui fico grato
Assunto:
função demanda
Autor:
ssousa3 - Seg Abr 04, 2011 14:30
Gente alguém por favor me ensine a calcular a fórmula da função demanda

Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
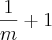 e
e 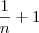 é:
é:![\frac{7+\sqrt[]{69}}{2} \frac{7+\sqrt[]{69}}{2}](/latexrender/pictures/a7cae91ca282913818f62f676df2f4a8.png)
![\frac{7-\sqrt[]{69}}{2} \frac{7-\sqrt[]{69}}{2}](/latexrender/pictures/6d49063d48d2a5a44132f9f164220d42.png)
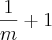
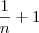


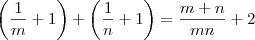 .
.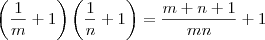 .
.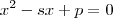 .
.
