-
-
Novo APOIA.se AjudaMatemática
por admin em Sáb Abr 25, 2020 19:01
- 0 Tópicos
- 480187 Mensagens
-
Última mensagem por admin

em Sáb Abr 25, 2020 19:01
-
-
Agradecimento aos Colaboradores
por admin em Qui Nov 15, 2018 00:25
- 0 Tópicos
- 539294 Mensagens
-
Última mensagem por admin

em Qui Nov 15, 2018 00:25
-
-
Ativação de Novos Registros
por admin em Qua Nov 14, 2018 11:58
- 0 Tópicos
- 503165 Mensagens
-
Última mensagem por admin

em Qua Nov 14, 2018 11:58
-
-
Regras do Fórum - Leia antes de postar!
por admin em Ter Mar 20, 2012 21:51
- 0 Tópicos
- 726800 Mensagens
-
Última mensagem por admin

em Ter Mar 20, 2012 21:51
-
-
DICA: Escrevendo Fórmulas com LaTeX via BBCode
por admin em Qua Ago 29, 2007 04:04
- 41 Tópicos
- 2162837 Mensagens
-
Última mensagem por Janayna

em Qui Abr 27, 2017 00:04
 por Molina » Qua Mai 20, 2009 23:15
por Molina » Qua Mai 20, 2009 23:15
Cleyson007 escreveu: ![-2(1-i\sqrt[2]{3})=n(1+i\sqrt[2]{3})-m -2(1-i\sqrt[2]{3})=n(1+i\sqrt[2]{3})-m](/latexrender/pictures/c0b2e318a42afeb35c03d4424718498c.png)
![-2(\frac{1-i\sqrt[2]{3}}{1+i\sqrt[2]{3}})=n-m -2(\frac{1-i\sqrt[2]{3}}{1+i\sqrt[2]{3}})=n-m](/latexrender/pictures/01e5dfa47975fbed84f0b8767fe11035.png)
Essa passagem eu acho que não está certa.
Por que o
![1+i\sqrt[2]{3} 1+i\sqrt[2]{3}](/latexrender/pictures/44b60452307bc3ab90dd2584f2dd3e1c.png)
não está multiplicando todo o lado direito da igualdade para passar pro lado direito dividindo. Certo?
To meio sem tempo, mas vou ver aqui alguma coisa e qualquer novidade coloco aqui!
Bom estudo,

Diego Molina |
CV |
FB |
.COMEquipe AjudaMatemática.com"Existem 10 tipos de pessoas: as que conhecem o sistema binário e as que não conhecem."
-

Molina
- Colaborador Moderador - Professor

-
- Mensagens: 1551
- Registrado em: Dom Jun 01, 2008 14:10
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura em Matemática - UFSC
- Andamento: formado
 por Cleyson007 » Qui Mai 21, 2009 09:23
por Cleyson007 » Qui Mai 21, 2009 09:23
Bom dia Molina!
Molina, realmente... quando postei a questão no fórum não percebi esse meu erro

Acho que o certo seria isolar a incógnita

e analisar os valores que atendem as condições
(número real).
Obrigado pela ajuda.
Um abraço
-

Cleyson007
- Colaborador Voluntário

-
- Mensagens: 1227
- Registrado em: Qua Abr 30, 2008 00:08
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Matemática UFJF
- Andamento: formado
 por -Tecno- » Qui Mai 28, 2009 23:38
por -Tecno- » Qui Mai 28, 2009 23:38
Oi Cleyson007! Me inscrevi no fórum agora para te responder e também participar desse fórum.

Eu comecei desde o início.
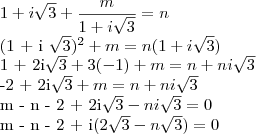
Agora é que vem o pulo do gato. Esse zero é o mesmo que

. Agora é só igualar a parte real com parte real e a imaginária com imaginária, tendo assim:
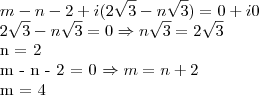 Resposta:
Resposta: 

Se você substituir lá em cima vai dar certinho.

Espero ter ajudado.
Abraços.
-
-Tecno-
- Novo Usuário

-
- Mensagens: 1
- Registrado em: Qui Mai 28, 2009 22:15
- Formação Escolar: ENSINO MÉDIO PROFISSIONALIZANTE
- Área/Curso: Eletrônica
- Andamento: cursando
 por Cleyson007 » Sex Mai 29, 2009 10:03
por Cleyson007 » Sex Mai 29, 2009 10:03
Olá -Tecno-!
Primeiramente, seja bem vindo ao Ajuda Matemática

aqui, aprendemos de maneira interativa

Gostei da resolução passo-a-passo.
Me ajudou bastante.
--> Espero poder ajudá-lo também

Um abraço.
-

Cleyson007
- Colaborador Voluntário

-
- Mensagens: 1227
- Registrado em: Qua Abr 30, 2008 00:08
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Matemática UFJF
- Andamento: formado
Voltar para Números Complexos
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Determine k
por Cleyson007 » Qui Jun 11, 2009 12:57
- 2 Respostas
- 2077 Exibições
- Última mensagem por DanielFerreira

Ter Set 22, 2009 13:19
Polinômios
-
- determine...
por lucianofloripa » Sex Nov 20, 2009 12:38
- 6 Respostas
- 4376 Exibições
- Última mensagem por lucianofloripa

Qui Nov 26, 2009 11:25
Geometria Analítica
-
- Determine MN
por Balanar » Seg Ago 30, 2010 01:36
- 0 Respostas
- 1051 Exibições
- Última mensagem por Balanar

Seg Ago 30, 2010 01:36
Álgebra Elementar
-
- determine a lei
por brunoscollaro » Sáb Out 22, 2011 11:58
- 1 Respostas
- 1159 Exibições
- Última mensagem por MarceloFantini

Sáb Out 22, 2011 15:16
Funções
-
- Determine a e b
por jcmatematica » Seg Ago 04, 2014 22:52
- 1 Respostas
- 3335 Exibições
- Última mensagem por Russman

Ter Ago 05, 2014 17:30
Polinômios
Usuários navegando neste fórum: Nenhum usuário registrado e 14 visitantes
Assunto:
[Função] do primeiro grau e quadratica
Autor:
Thassya - Sáb Out 01, 2011 16:20
1) Para que os pontos (1,3) e (-3,1) pertençam ao grafico da função f(X)=ax + b ,o valor de b-a deve ser ?
2)Qual o maior valor assumido pela função f : [-7 ,10] em R definida por f(x) = x ao quadrado - 5x + 9?
3) A função f, do primeiro grau, é definida pos f(x)= 3x + k para que o gráfico de f corte o eixo das ordenadas no ponto de ordenada 5 é?
Assunto:
[Função] do primeiro grau e quadratica
Autor:
Neperiano - Sáb Out 01, 2011 19:46
Ola
Qual as suas dúvidas?
O que você não está conseguindo fazer?
Nos mostre para podermos ajudar
Atenciosamente
Assunto:
[Função] do primeiro grau e quadratica
Autor:
joaofonseca - Sáb Out 01, 2011 20:15
1)Dados dois pontos A=(1,3) e B=(-3,1) de uma reta, é possivel definir a sua equação.


Em

substitui-se
m, substitui-se
y e
x por um dos pares ordenados, e resolve-se em ordem a
b.

2)Na equação

não existem zeros.Senão vejamos
Completando o quadrado,

As coordenadas do vertice da parabola são

O eixo de simetria é a reta

.Como se pode observar o vertice está acima do eixo Ox, estando parabola virada para cima, o vertice é um mínimo absoluto.Então basta calcular a função para os valores dos extremos do intervalo.
f(-7)=93
f(10)=59
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
 e
e  reais para que
reais para que ![1+i\sqrt[2]{3}+\frac{m}{1+i\sqrt[2]{3}}=n 1+i\sqrt[2]{3}+\frac{m}{1+i\sqrt[2]{3}}=n](/latexrender/pictures/2f8b061ac4bfbffa9a20f7d2da95f480.png) .
.![({1+i\sqrt[2]{3}})^{2}+m=(1+i\sqrt[2]{3})(n) ({1+i\sqrt[2]{3}})^{2}+m=(1+i\sqrt[2]{3})(n)](/latexrender/pictures/50709373137a418093e845a43c687a7d.png)
![(1+i\sqrt[2]{3})(1+i\sqrt[2]{3})+m=(1+i\sqrt[2]{3})(n) (1+i\sqrt[2]{3})(1+i\sqrt[2]{3})+m=(1+i\sqrt[2]{3})(n)](/latexrender/pictures/2ce93c9f105fcd53cf787ba1b5a89c7f.png)
![1+i\sqrt[2]{3}+i\sqrt[2]{3}+{i}^{2}({\sqrt[2]{3}})^{2}+m=n+in\sqrt[2]{3} 1+i\sqrt[2]{3}+i\sqrt[2]{3}+{i}^{2}({\sqrt[2]{3}})^{2}+m=n+in\sqrt[2]{3}](/latexrender/pictures/b9a060eef24438a6ac8cd7699b31cd9f.png)
![1+2i\sqrt[2]{3}+(-3)+m=n(1+i\sqrt[2]{3}) 1+2i\sqrt[2]{3}+(-3)+m=n(1+i\sqrt[2]{3})](/latexrender/pictures/85187ce5c7e982362de3676b447009a0.png)
![1+2i\sqrt[2]{3}-3+m=n(1+i\sqrt[2]{3}) 1+2i\sqrt[2]{3}-3+m=n(1+i\sqrt[2]{3})](/latexrender/pictures/aea94fe8d1b2116cc7e4545c8d264b7d.png)
![-2(1-i\sqrt[2]{3})+m=n(1+i\sqrt[2]{3}) -2(1-i\sqrt[2]{3})+m=n(1+i\sqrt[2]{3})](/latexrender/pictures/863125ef85df1270ff2210444398a747.png)
![-2(1-i\sqrt[2]{3})=n(1+i\sqrt[2]{3})-m -2(1-i\sqrt[2]{3})=n(1+i\sqrt[2]{3})-m](/latexrender/pictures/c0b2e318a42afeb35c03d4424718498c.png)
![-2(\frac{1-i\sqrt[2]{3}}{1+i\sqrt[2]{3}})=n-m -2(\frac{1-i\sqrt[2]{3}}{1+i\sqrt[2]{3}})=n-m](/latexrender/pictures/01e5dfa47975fbed84f0b8767fe11035.png)
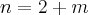


 e
e  reais para que
reais para que ![1+i\sqrt[2]{3}+\frac{m}{1+i\sqrt[2]{3}}=n 1+i\sqrt[2]{3}+\frac{m}{1+i\sqrt[2]{3}}=n](/latexrender/pictures/2f8b061ac4bfbffa9a20f7d2da95f480.png) .
.![({1+i\sqrt[2]{3}})^{2}+m=(1+i\sqrt[2]{3})(n) ({1+i\sqrt[2]{3}})^{2}+m=(1+i\sqrt[2]{3})(n)](/latexrender/pictures/50709373137a418093e845a43c687a7d.png)
![(1+i\sqrt[2]{3})(1+i\sqrt[2]{3})+m=(1+i\sqrt[2]{3})(n) (1+i\sqrt[2]{3})(1+i\sqrt[2]{3})+m=(1+i\sqrt[2]{3})(n)](/latexrender/pictures/2ce93c9f105fcd53cf787ba1b5a89c7f.png)
![1+i\sqrt[2]{3}+i\sqrt[2]{3}+{i}^{2}({\sqrt[2]{3}})^{2}+m=n+in\sqrt[2]{3} 1+i\sqrt[2]{3}+i\sqrt[2]{3}+{i}^{2}({\sqrt[2]{3}})^{2}+m=n+in\sqrt[2]{3}](/latexrender/pictures/b9a060eef24438a6ac8cd7699b31cd9f.png)
![1+2i\sqrt[2]{3}+(-3)+m=n(1+i\sqrt[2]{3}) 1+2i\sqrt[2]{3}+(-3)+m=n(1+i\sqrt[2]{3})](/latexrender/pictures/85187ce5c7e982362de3676b447009a0.png)
![1+2i\sqrt[2]{3}-3+m=n(1+i\sqrt[2]{3}) 1+2i\sqrt[2]{3}-3+m=n(1+i\sqrt[2]{3})](/latexrender/pictures/aea94fe8d1b2116cc7e4545c8d264b7d.png)
![-2(1-i\sqrt[2]{3})+m=n(1+i\sqrt[2]{3}) -2(1-i\sqrt[2]{3})+m=n(1+i\sqrt[2]{3})](/latexrender/pictures/863125ef85df1270ff2210444398a747.png)
![-2(1-i\sqrt[2]{3})=n(1+i\sqrt[2]{3})-m -2(1-i\sqrt[2]{3})=n(1+i\sqrt[2]{3})-m](/latexrender/pictures/c0b2e318a42afeb35c03d4424718498c.png)
![-2(\frac{1-i\sqrt[2]{3}}{1+i\sqrt[2]{3}})=n-m -2(\frac{1-i\sqrt[2]{3}}{1+i\sqrt[2]{3}})=n-m](/latexrender/pictures/01e5dfa47975fbed84f0b8767fe11035.png)
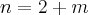


![1+i\sqrt[2]{3} 1+i\sqrt[2]{3}](/latexrender/pictures/44b60452307bc3ab90dd2584f2dd3e1c.png) não está multiplicando todo o lado direito da igualdade para passar pro lado direito dividindo. Certo?
não está multiplicando todo o lado direito da igualdade para passar pro lado direito dividindo. Certo?


 e analisar os valores que atendem as condições (número real).
e analisar os valores que atendem as condições (número real).
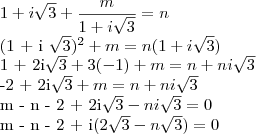
 . Agora é só igualar a parte real com parte real e a imaginária com imaginária, tendo assim:
. Agora é só igualar a parte real com parte real e a imaginária com imaginária, tendo assim: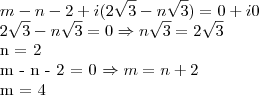



 aqui, aprendemos de maneira interativa
aqui, aprendemos de maneira interativa 




 substitui-se m, substitui-se y e x por um dos pares ordenados, e resolve-se em ordem a b.
substitui-se m, substitui-se y e x por um dos pares ordenados, e resolve-se em ordem a b.
 não existem zeros.Senão vejamos
não existem zeros.Senão vejamos

 .Como se pode observar o vertice está acima do eixo Ox, estando parabola virada para cima, o vertice é um mínimo absoluto.Então basta calcular a função para os valores dos extremos do intervalo.
.Como se pode observar o vertice está acima do eixo Ox, estando parabola virada para cima, o vertice é um mínimo absoluto.Então basta calcular a função para os valores dos extremos do intervalo.