 por cristina » Qui Set 09, 2010 09:57
por cristina » Qui Set 09, 2010 09:57
Bom dia, preciso de ajuda, não lembro como desenvolver potencia com fração...
Assinale todos os valores das raizes de
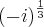
-
cristina
- Usuário Parceiro

-
- Mensagens: 82
- Registrado em: Qua Set 02, 2009 17:49
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura/ matematica
- Andamento: cursando
 por MarceloFantini » Qui Set 09, 2010 14:21
por MarceloFantini » Qui Set 09, 2010 14:21
O que você quer é isto:
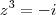
? Caso contrário:
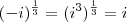
.
Futuro MATEMÁTICO
-
MarceloFantini
- Colaborador Moderador

-
- Mensagens: 3126
- Registrado em: Seg Dez 14, 2009 11:41
- Formação Escolar: GRADUAÇÃO
- Andamento: formado
 por cristina » Qui Set 09, 2010 16:56
por cristina » Qui Set 09, 2010 16:56
Então Fantini, na correria acabei de colocar as alternativas....
a)
![\frac{1}{2}(-\sqrt[]{3}+ i) \frac{1}{2}(-\sqrt[]{3}+ i)](/latexrender/pictures/8732f11eff22fed70ba7f3a51b15d561.png)
b)
![\frac{1}{2}(\sqrt[]{3}- i) \frac{1}{2}(\sqrt[]{3}- i)](/latexrender/pictures/4f13ee524f0cd3c36bf77285bade463b.png)
c)
![\frac{1}{2}(\sqrt[]{3}+ i) \frac{1}{2}(\sqrt[]{3}+ i)](/latexrender/pictures/03480d20d76b0a134f616b230eafae59.png)
d)
![\frac{1}{2}(-\sqrt[]{3}- i) \frac{1}{2}(-\sqrt[]{3}- i)](/latexrender/pictures/5694fea069c9c46edecaf8124f24c38e.png)
e) i
f) - i
No exercicio pede pra assinalr os valores das raizes... tem mais de uma? neste caso...
-
cristina
- Usuário Parceiro

-
- Mensagens: 82
- Registrado em: Qua Set 02, 2009 17:49
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura/ matematica
- Andamento: cursando
Voltar para Números Complexos
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [raízes de números complexos] Raízes de uma equação com grau
por karenfreitas » Seg Ago 22, 2016 19:08
- 1 Respostas
- 8120 Exibições
- Última mensagem por adauto martins

Sáb Ago 27, 2016 16:11
Números Complexos
-
- [Radiciação] Raízes dentro de raízes
por mottasky » Ter Set 13, 2011 22:00
- 2 Respostas
- 2577 Exibições
- Última mensagem por mottasky

Qui Set 15, 2011 15:52
Álgebra Elementar
-
- raízes.
por carolina camargo » Qua Jun 17, 2009 16:39
- 5 Respostas
- 2954 Exibições
- Última mensagem por Molina

Qua Jun 17, 2009 19:01
Funções
-
- Raízes
por aline2010 » Dom Ago 08, 2010 07:46
- 1 Respostas
- 1328 Exibições
- Última mensagem por MarceloFantini

Seg Ago 09, 2010 06:08
Sistemas de Equações
-
- RAIZES
por vanessitah » Sáb Mar 05, 2011 20:36
- 12 Respostas
- 6477 Exibições
- Última mensagem por Abelardo

Seg Mar 07, 2011 13:48
Álgebra Elementar
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
(FGV) ... função novamente rs
Autor:
my2009 - Qua Dez 08, 2010 21:48
Uma função polinomial f do 1° grau é tal que f(3) = 6 e f(4) = 8.Portanto o valor de f(10) é :
Assunto:
(FGV) ... função novamente rs
Autor: Anonymous - Qui Dez 09, 2010 17:25
Uma função de 1º grau é dada por

.
Temos que para

,

e para

,

.

Ache o valor de

e

, monte a função e substitua

por

.
Assunto:
(FGV) ... função novamente rs
Autor:
Pinho - Qui Dez 16, 2010 13:57
my2009 escreveu:Uma função polinomial f do 1° grau é tal que f(3) = 6 e f(4) = 8.Portanto o valor de f(10) é :
f(x)= 2.x
f(3)=2.3=6
f(4)=2.4=8
f(10)=2.10=20
Assunto:
(FGV) ... função novamente rs
Autor:
dagoth - Sex Dez 17, 2010 11:55
isso ai foi uma questao da FGV?
haahua to precisando trocar de faculdade.
Assunto:
(FGV) ... função novamente rs
Autor:
Thiago 86 - Qua Mar 06, 2013 23:11
Saudações!

ví suaquestão e tentei resolver, depois você conta-me se eu acertei.
Uma função de 1º grau é dada por y=3a+b
Resposta :
3a+b=6 x(4)
4a+b=8 x(-3)
12a+4b=24
-12a-3b=-24
b=0
substituindo b na 1°, ttenho que: 3a+b=6
3a+0=6
a=2
substituindo em: y=3a+b
y=30+0
y=30

Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
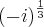


![\frac{1}{2}(-\sqrt[]{3}+ i) \frac{1}{2}(-\sqrt[]{3}+ i)](/latexrender/pictures/8732f11eff22fed70ba7f3a51b15d561.png)
![\frac{1}{2}(\sqrt[]{3}- i) \frac{1}{2}(\sqrt[]{3}- i)](/latexrender/pictures/4f13ee524f0cd3c36bf77285bade463b.png)
![\frac{1}{2}(\sqrt[]{3}+ i) \frac{1}{2}(\sqrt[]{3}+ i)](/latexrender/pictures/03480d20d76b0a134f616b230eafae59.png)
![\frac{1}{2}(-\sqrt[]{3}- i) \frac{1}{2}(-\sqrt[]{3}- i)](/latexrender/pictures/5694fea069c9c46edecaf8124f24c38e.png)

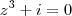 disfarçadamente. Veja:
disfarçadamente. Veja: 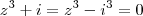 . Fatorando:
. Fatorando: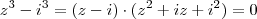
 . Vamos às outras:
. Vamos às outras: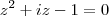
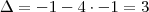
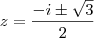
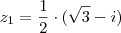
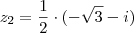


 .
. ,
,  e para
e para  ,
,  .
.
 e
e  , monte a função e substitua
, monte a função e substitua  por
por  .
.
