-
-
Novo APOIA.se AjudaMatemática
por admin em Sáb Abr 25, 2020 19:01
- 0 Tópicos
- 480652 Mensagens
-
Última mensagem por admin

em Sáb Abr 25, 2020 19:01
-
-
Agradecimento aos Colaboradores
por admin em Qui Nov 15, 2018 00:25
- 0 Tópicos
- 542086 Mensagens
-
Última mensagem por admin

em Qui Nov 15, 2018 00:25
-
-
Ativação de Novos Registros
por admin em Qua Nov 14, 2018 11:58
- 0 Tópicos
- 505810 Mensagens
-
Última mensagem por admin

em Qua Nov 14, 2018 11:58
-
-
Regras do Fórum - Leia antes de postar!
por admin em Ter Mar 20, 2012 21:51
- 0 Tópicos
- 734301 Mensagens
-
Última mensagem por admin

em Ter Mar 20, 2012 21:51
-
-
DICA: Escrevendo Fórmulas com LaTeX via BBCode
por admin em Qua Ago 29, 2007 04:04
- 41 Tópicos
- 2178479 Mensagens
-
Última mensagem por Janayna

em Qui Abr 27, 2017 00:04
 por karenfreitas » Dom Dez 04, 2016 16:31
por karenfreitas » Dom Dez 04, 2016 16:31
Seja
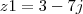
e
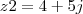
. Ache o valor de
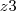
.

Estou com dificuldades quando aparece essa fração elevando os números
complexos. Se alguém puder fazer passo a passo agradeço.
Coloquei em anexo a tentativa do que comecei a fazer.
- Anexos
-

- Sem Título-1.png (115.38 KiB) Exibido 9011 vezes
-
karenfreitas
- Usuário Ativo

-
- Mensagens: 12
- Registrado em: Qua Mai 04, 2016 14:20
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia
- Andamento: cursando
 por Cleyson007 » Seg Dez 05, 2016 20:28
por Cleyson007 » Seg Dez 05, 2016 20:28
Boa noite Karen!
Qual a sua dúvida especificamente?
A fração 1/3 significa calcular a raiz cúbica do número
complexo z
2. O 1/2 que aparece no símbolo chave significa que deverá ser calculada a raiz quadrada do resultado.
Sou professor de Matemática e trabalho resolvendo exercícios a um custo bastante acessível e ótimo prazo para entrega.
Caso queira conhecer melhor o meu trabalho me mande um e-mail ou me chame no WhatsApp por favor.
E-mail:
descomplicamat@hotmail.comWhatsApp: (38) 9 9889-5755
Qualquer dúvida estou a disposição.
Atenciosamente,
Prof. Clésio
-

Cleyson007
- Colaborador Voluntário

-
- Mensagens: 1227
- Registrado em: Qua Abr 30, 2008 00:08
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Matemática UFJF
- Andamento: formado
Voltar para Números Complexos
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Números complexos módulo de dois números complexos important
por elisamaria » Qui Jun 11, 2015 16:56
- 1 Respostas
- 15589 Exibições
- Última mensagem por nakagumahissao

Qui Jun 11, 2015 19:20
Números Complexos
-
- Numeros complexos!
por Estela » Seg Mar 17, 2008 00:57
- 7 Respostas
- 11540 Exibições
- Última mensagem por andegledson

Seg Nov 02, 2009 21:41
Números Complexos
-
- Números Complexos
por michelle » Dom Ago 31, 2008 15:35
- 3 Respostas
- 8967 Exibições
- Última mensagem por admin

Dom Ago 31, 2008 21:00
Números Complexos
-
- Números Complexos
por Cleyson007 » Qui Mai 14, 2009 13:57
- 7 Respostas
- 11101 Exibições
- Última mensagem por Cleyson007

Sáb Mai 16, 2009 11:04
Números Complexos
-
- NUMEROS COMPLEXOS
por lieberth » Sáb Jun 13, 2009 13:48
- 1 Respostas
- 3681 Exibições
- Última mensagem por Marcampucio

Sáb Jun 13, 2009 14:35
Números Complexos
Usuários navegando neste fórum: Nenhum usuário registrado e 13 visitantes
Assunto:
Unesp - 95 Números Complexos
Autor:
Alucard014 - Dom Ago 01, 2010 18:22
(UNESP - 95) Seja L o Afixo de um Número complexo

em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto.
Assunto:
Unesp - 95 Números Complexos
Autor:
MarceloFantini - Qui Ago 05, 2010 17:27
Seja

o ângulo entre o eixo horizontal e o afixo

. O triângulo é retângulo com catetos

e

, tal que

. Seja

o ângulo complementar. Então

. Como

, o ângulo que o afixo

formará com a horizontal será

, mas negativo pois tem de ser no quarto quadrante. Se

, então

. Como módulo é um:

.
Logo, o afixo é

.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
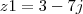 e
e 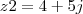 . Ache o valor de
. Ache o valor de 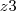 .
.

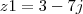 e
e 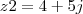 . Ache o valor de
. Ache o valor de 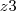 .
.


 em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto.
em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto. o ângulo entre o eixo horizontal e o afixo
o ângulo entre o eixo horizontal e o afixo  . O triângulo é retângulo com catetos
. O triângulo é retângulo com catetos  e
e  , tal que
, tal que  . Seja
. Seja  o ângulo complementar. Então
o ângulo complementar. Então  . Como
. Como  , o ângulo que o afixo
, o ângulo que o afixo  formará com a horizontal será
formará com a horizontal será  , mas negativo pois tem de ser no quarto quadrante. Se
, mas negativo pois tem de ser no quarto quadrante. Se  , então
, então  . Como módulo é um:
. Como módulo é um:  .
. .
.