-
-
Novo APOIA.se AjudaMatemática
por admin em Sáb Abr 25, 2020 19:01
- 0 Tópicos
- 477893 Mensagens
-
Última mensagem por admin

em Sáb Abr 25, 2020 19:01
-
-
Agradecimento aos Colaboradores
por admin em Qui Nov 15, 2018 00:25
- 0 Tópicos
- 529631 Mensagens
-
Última mensagem por admin

em Qui Nov 15, 2018 00:25
-
-
Ativação de Novos Registros
por admin em Qua Nov 14, 2018 11:58
- 0 Tópicos
- 493168 Mensagens
-
Última mensagem por admin

em Qua Nov 14, 2018 11:58
-
-
Regras do Fórum - Leia antes de postar!
por admin em Ter Mar 20, 2012 21:51
- 0 Tópicos
- 699368 Mensagens
-
Última mensagem por admin

em Ter Mar 20, 2012 21:51
-
-
DICA: Escrevendo Fórmulas com LaTeX via BBCode
por admin em Qua Ago 29, 2007 04:04
- 41 Tópicos
- 2110067 Mensagens
-
Última mensagem por Janayna

em Qui Abr 27, 2017 00:04
 por karenfreitas » Seg Ago 22, 2016 19:08
por karenfreitas » Seg Ago 22, 2016 19:08
Resolva a equação:

Agradeço a ajuda prestada para como proceder com essa questão.
-
karenfreitas
- Usuário Ativo

-
- Mensagens: 12
- Registrado em: Qua Mai 04, 2016 14:20
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia
- Andamento: cursando
 por adauto martins » Sáb Ago 27, 2016 16:11
por adauto martins » Sáb Ago 27, 2016 16:11
temos um polinomio de quarto grau(4 raizes reais ou complexas)com coeficientes de num.inteiros,logo teremos
q. existe pelo menos um
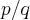
onde
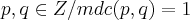
,ou seja primos entre si...essa ou essas raizes sairao dos divisores de
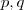
...onde
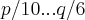
...logo o conjunto onde ha possibilidade de termos uma raiz sera:
{
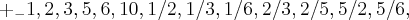
}...o raio de existencia das possiveis raizes é dado por:
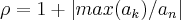
p/
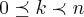
...em nosso caso
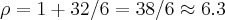
...[
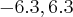
]...entao do conj. das possiveis raizes tiramos apenas o num.

...e agora é testar uma por uma e encontrar uma ou mais raizes racionais...se

,ai faremos q.

,ou seja vai baixando o grau do polinomio,ate chegarmos a um polinomio de segundo grau,onde possivelmente encontraremos raizes reais ou complexas...é pór ai,nao é facil,é calculo e calculos...maos a obra...
-
adauto martins
- Colaborador Voluntário

-
- Mensagens: 1171
- Registrado em: Sex Set 05, 2014 19:37
- Formação Escolar: EJA
- Área/Curso: matematica
- Andamento: cursando
Voltar para Números Complexos
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Raízes de números complexos
por Rennannn » Qua Fev 27, 2013 10:27
- 8 Respostas
- 5032 Exibições
- Última mensagem por natanaelskt

Qua Mar 27, 2013 14:18
Números Complexos
-
- Raizes de equação de grau>=3
por spyderkill » Qua Mai 09, 2012 17:31
- 2 Respostas
- 2135 Exibições
- Última mensagem por pedroaugustox47

Sex Mai 11, 2012 02:33
Polinômios
-
- Raizes de equação de grau>=3
por citadp » Qua Jun 20, 2012 09:32
- 3 Respostas
- 1964 Exibições
- Última mensagem por Russman

Sex Jul 06, 2012 15:49
Cálculo: Limites, Derivadas e Integrais
-
- Raizes da equaçao do 2° grau
por hissamo » Sex Abr 10, 2015 15:57
- 1 Respostas
- 1556 Exibições
- Última mensagem por DanielFerreira

Sáb Abr 11, 2015 17:14
Equações
-
- Raizes de uma equação de terceiro grau.
por 380625 » Dom Mar 27, 2011 13:58
- 3 Respostas
- 2651 Exibições
- Última mensagem por MarceloFantini

Dom Mar 27, 2011 18:09
Funções
Usuários navegando neste fórum: Nenhum usuário registrado e 6 visitantes
Assunto:
[Função] do primeiro grau e quadratica
Autor:
Thassya - Sáb Out 01, 2011 16:20
1) Para que os pontos (1,3) e (-3,1) pertençam ao grafico da função f(X)=ax + b ,o valor de b-a deve ser ?
2)Qual o maior valor assumido pela função f : [-7 ,10] em R definida por f(x) = x ao quadrado - 5x + 9?
3) A função f, do primeiro grau, é definida pos f(x)= 3x + k para que o gráfico de f corte o eixo das ordenadas no ponto de ordenada 5 é?
Assunto:
[Função] do primeiro grau e quadratica
Autor:
Neperiano - Sáb Out 01, 2011 19:46
Ola
Qual as suas dúvidas?
O que você não está conseguindo fazer?
Nos mostre para podermos ajudar
Atenciosamente
Assunto:
[Função] do primeiro grau e quadratica
Autor:
joaofonseca - Sáb Out 01, 2011 20:15
1)Dados dois pontos A=(1,3) e B=(-3,1) de uma reta, é possivel definir a sua equação.


Em

substitui-se
m, substitui-se
y e
x por um dos pares ordenados, e resolve-se em ordem a
b.

2)Na equação

não existem zeros.Senão vejamos
Completando o quadrado,

As coordenadas do vertice da parabola são

O eixo de simetria é a reta

.Como se pode observar o vertice está acima do eixo Ox, estando parabola virada para cima, o vertice é um mínimo absoluto.Então basta calcular a função para os valores dos extremos do intervalo.
f(-7)=93
f(10)=59
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.




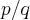 onde
onde 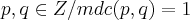 ,ou seja primos entre si...essa ou essas raizes sairao dos divisores de
,ou seja primos entre si...essa ou essas raizes sairao dos divisores de 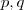 ...onde
...onde 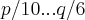 ...logo o conjunto onde ha possibilidade de termos uma raiz sera:
...logo o conjunto onde ha possibilidade de termos uma raiz sera: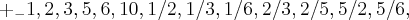 }...o raio de existencia das possiveis raizes é dado por:
}...o raio de existencia das possiveis raizes é dado por: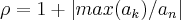 p/
p/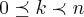 ...em nosso caso
...em nosso caso 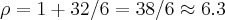 ...[
...[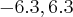 ]...entao do conj. das possiveis raizes tiramos apenas o num.
]...entao do conj. das possiveis raizes tiramos apenas o num. ...e agora é testar uma por uma e encontrar uma ou mais raizes racionais...se
...e agora é testar uma por uma e encontrar uma ou mais raizes racionais...se  ,ai faremos q.
,ai faremos q.  ,ou seja vai baixando o grau do polinomio,ate chegarmos a um polinomio de segundo grau,onde possivelmente encontraremos raizes reais ou complexas...é pór ai,nao é facil,é calculo e calculos...maos a obra...
,ou seja vai baixando o grau do polinomio,ate chegarmos a um polinomio de segundo grau,onde possivelmente encontraremos raizes reais ou complexas...é pór ai,nao é facil,é calculo e calculos...maos a obra...


 substitui-se m, substitui-se y e x por um dos pares ordenados, e resolve-se em ordem a b.
substitui-se m, substitui-se y e x por um dos pares ordenados, e resolve-se em ordem a b.
 não existem zeros.Senão vejamos
não existem zeros.Senão vejamos

 .Como se pode observar o vertice está acima do eixo Ox, estando parabola virada para cima, o vertice é um mínimo absoluto.Então basta calcular a função para os valores dos extremos do intervalo.
.Como se pode observar o vertice está acima do eixo Ox, estando parabola virada para cima, o vertice é um mínimo absoluto.Então basta calcular a função para os valores dos extremos do intervalo.