Olá a todos,
Numa resolução de sistema de equações racionais é necessário igualar o denominador a zero. O valor no denominador é 15x³(x-4). Então temos que fazer 15x³ = 0 que fica igual a x=0.
O que não percebi!
Consigo perceber que o 15 passa de multiplicar para o outro lado a dividir. E zero a dividir por alguma coisa é igual a zero. Mas como fazo com a potencia que fica no x. Aquele expoente como desaparece?
Outra questão:
Porque que "divido" a expressão 15x³(x-4) em dois? Não deveria aplicar a dsitribuitiva para resolver e no final igualar a zero para descobrir o valor de x? Ficaria algo deste genero:
15x³(x-4)
15x?-60x³=0
...
Isto não tem lógica, certo? Estou a colocar o meu raciocinio aqui mesmo para testar as coisas :P Eu por vezes penso demasiado fora da caixa!


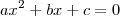 , onde
, onde  . Considere a equação de grau 2 em que
. Considere a equação de grau 2 em que  , daí ficamos com
, daí ficamos com 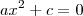 ; tal equação também é do 2º grau, mas incompleta.
; tal equação também é do 2º grau, mas incompleta.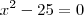 . Para encontrar suas raízes fazemos:
. Para encontrar suas raízes fazemos:![\\ x^2 - 25 = 0 \\ x^2 = 25 \\ x = \sqrt[2]{25} \\ \boxed{x = \pm 5} \\ x^2 - 25 = 0 \\ x^2 = 25 \\ x = \sqrt[2]{25} \\ \boxed{x = \pm 5}](/latexrender/pictures/af5022c7685bb6dd25b235fe035f7c58.png)
![\\ 15x^3 = 0 \\\\ x^3 = \frac{0}{15} \\\\ x^3 = 0 \\\\ x = \sqrt[3]{0} \\\\ \boxed{x = 0} \\ 15x^3 = 0 \\\\ x^3 = \frac{0}{15} \\\\ x^3 = 0 \\\\ x = \sqrt[3]{0} \\\\ \boxed{x = 0}](/latexrender/pictures/d0931c10e63ef3310759ab4bb10e472a.png)
 , isto é,
, isto é, 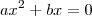 .
. em evidência. Prefiro este, pois reduz a resolução em algumas linhas, por conseguinte, a chance de cometer alguma distração é menor.
em evidência. Prefiro este, pois reduz a resolução em algumas linhas, por conseguinte, a chance de cometer alguma distração é menor.


![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]} {(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]}](/latexrender/pictures/19807748a214d3361336324f3e43ea9a.png)
![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}} {(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}}](/latexrender/pictures/3d7908e5b4e397bf635b6546063d9130.png)

 , ou seja, 1 dividido por 20 é igual a 0.05 . Sendo assim, a função final é igual a vinte elevado à meio.
, ou seja, 1 dividido por 20 é igual a 0.05 . Sendo assim, a função final é igual a vinte elevado à meio. ![{0,05}^{-\frac{1}{2}} = {\frac{1}{20}}^{-\frac{1}{2}} = {\frac{20}{1}}^{\frac{1}{2}} = \sqrt[2]{20} {0,05}^{-\frac{1}{2}} = {\frac{1}{20}}^{-\frac{1}{2}} = {\frac{20}{1}}^{\frac{1}{2}} = \sqrt[2]{20}](/latexrender/pictures/c0100c6f4d8bdbb7d54165e6be7aff04.png)
 da seguinte forma:
da seguinte forma: .
. da seguinte forma:
da seguinte forma: .
.