I)
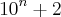
II)
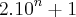
III)
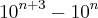
Quais são divisíveis por 6?
a) Apenas II e III
b) Apenas I e II
c) Apenas III
d) Apenas I
e) Apenas I e III

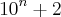
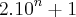
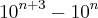

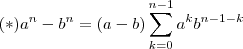 obtemos , para
obtemos , para 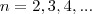
![10^n + 2 = (10^n - 1^n) + 3 = 3 + 9 \sum_{k=0}^{n-1} 10^k = 3 + 9 + 9 \sum_{k=1}^{n-1} 2^k \cdot 5^k = 6 \cdot (2 + 3 \sum_{k=1}^{n-1} 2^{k-1} \cdot 5^{k} ) = 6(2 + 3[5 + 50 + 500 + \cdots + 2^{n-2} \cdot 10^{n-1} ] 10^n + 2 = (10^n - 1^n) + 3 = 3 + 9 \sum_{k=0}^{n-1} 10^k = 3 + 9 + 9 \sum_{k=1}^{n-1} 2^k \cdot 5^k = 6 \cdot (2 + 3 \sum_{k=1}^{n-1} 2^{k-1} \cdot 5^{k} ) = 6(2 + 3[5 + 50 + 500 + \cdots + 2^{n-2} \cdot 10^{n-1} ]](/latexrender/pictures/7dac550e4104327b5feae1a7cca2ba5e.png) .
.  se ele for simultaneamente por 3 e 2 , claro . No mínimo ele é par , logo o último digito dele é 0,2,4,6,8 .Agora ,se ele for divisível por
se ele for simultaneamente por 3 e 2 , claro . No mínimo ele é par , logo o último digito dele é 0,2,4,6,8 .Agora ,se ele for divisível por  , investigamos certas propriedades . Escreva
, investigamos certas propriedades . Escreva 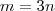 (m,n inteiros ) . Podemos representar
(m,n inteiros ) . Podemos representar  por
por 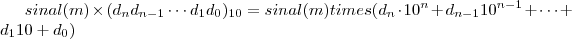 onde os
onde os 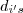 variam de
variam de  a
a 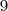 .
. 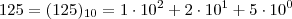 .Segue
.Segue 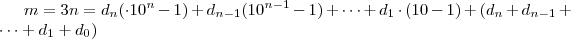 . Graças a fatoração
. Graças a fatoração 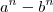 cada parcela
cada parcela 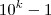 é divisível por 3 , e com isso a soma dos dígitos também o é .Alternativamente
é divisível por 3 , e com isso a soma dos dígitos também o é .Alternativamente 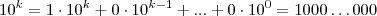
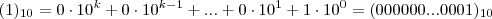 . Fazendo a subtração de números de mesma base , temos
. Fazendo a subtração de números de mesma base , temos 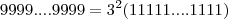 .Logo a soma dos dígitos também são divisível por
.Logo a soma dos dígitos também são divisível por  .
. 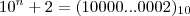 . O último dígito é 2
. O último dígito é 2  número é par
número é par  divisível por
divisível por  .
.  divisível por
divisível por  .
. ![\therefore [(i) \wedge (ii) ] \implies 6 | (10^n+2) \therefore [(i) \wedge (ii) ] \implies 6 | (10^n+2)](/latexrender/pictures/b09cd341454340de4b7533c581d2d958.png) .
.
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]} {(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]}](/latexrender/pictures/19807748a214d3361336324f3e43ea9a.png)
![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}} {(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}}](/latexrender/pictures/3d7908e5b4e397bf635b6546063d9130.png)
zig escreveu:

 , ou seja, 1 dividido por 20 é igual a 0.05 . Sendo assim, a função final é igual a vinte elevado à meio.
, ou seja, 1 dividido por 20 é igual a 0.05 . Sendo assim, a função final é igual a vinte elevado à meio. ![{0,05}^{-\frac{1}{2}} = {\frac{1}{20}}^{-\frac{1}{2}} = {\frac{20}{1}}^{\frac{1}{2}} = \sqrt[2]{20} {0,05}^{-\frac{1}{2}} = {\frac{1}{20}}^{-\frac{1}{2}} = {\frac{20}{1}}^{\frac{1}{2}} = \sqrt[2]{20}](/latexrender/pictures/c0100c6f4d8bdbb7d54165e6be7aff04.png)
 da seguinte forma:
da seguinte forma: .
. da seguinte forma:
da seguinte forma: .
.