-
-
Novo APOIA.se AjudaMatemática
por admin em Sáb Abr 25, 2020 19:01
- 0 Tópicos
- 478720 Mensagens
-
Última mensagem por admin

em Sáb Abr 25, 2020 19:01
-
-
Agradecimento aos Colaboradores
por admin em Qui Nov 15, 2018 00:25
- 0 Tópicos
- 534918 Mensagens
-
Última mensagem por admin

em Qui Nov 15, 2018 00:25
-
-
Ativação de Novos Registros
por admin em Qua Nov 14, 2018 11:58
- 0 Tópicos
- 498527 Mensagens
-
Última mensagem por admin

em Qua Nov 14, 2018 11:58
-
-
Regras do Fórum - Leia antes de postar!
por admin em Ter Mar 20, 2012 21:51
- 0 Tópicos
- 714655 Mensagens
-
Última mensagem por admin

em Ter Mar 20, 2012 21:51
-
-
DICA: Escrevendo Fórmulas com LaTeX via BBCode
por admin em Qua Ago 29, 2007 04:04
- 41 Tópicos
- 2137233 Mensagens
-
Última mensagem por Janayna

em Qui Abr 27, 2017 00:04
 por mota_16 » Sáb Dez 28, 2013 23:10
por mota_16 » Sáb Dez 28, 2013 23:10
Nesse caso, como faço para descrever geometricamente. Percebi que tenho uma soma de distâncias, mas não consegui avançar.
O subconjunto do plano complexo
![A=\left[z\in C/\left|z-i \right|+\left|z+i \right|=1 \right] A=\left[z\in C/\left|z-i \right|+\left|z+i \right|=1 \right]](/latexrender/pictures/b900fa797329be59a938e05fa7fad417.png)
deve ser descrito geometricamente como:
a) uma circunferência
b) uma hipérbole
c) uma elipse
d) uma parábola
e) duas retas
-
mota_16
- Usuário Ativo

-
- Mensagens: 19
- Registrado em: Sex Dez 06, 2013 10:36
- Formação Escolar: ENSINO MÉDIO
- Área/Curso: Regular
- Andamento: cursando
 por e8group » Dom Dez 29, 2013 16:50
por e8group » Dom Dez 29, 2013 16:50
Um número complexo

se exprimir por
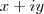
(x,y sobre

) . Agora suponha que
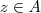
,então a propriedade
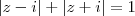
é verdadeira e substituindo z por
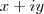
,obterá a soma de módulos de dois números complexos . Lembre-se
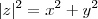
.
Agora tente concluir .
-
e8group
- Colaborador Voluntário

-
- Mensagens: 1400
- Registrado em: Sex Jun 01, 2012 12:10
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica
- Andamento: cursando
 por mota_16 » Seg Dez 30, 2013 14:42
por mota_16 » Seg Dez 30, 2013 14:42
Santhiago eu substituí e obtive:
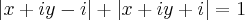
Pensei em colocar i em evidência:
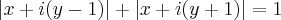
Como
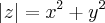
. Pensei em elevar ambos os membros ao quadrado, mas encontrei resultados que não me ajudaram. É isso? Esse é o caminho?
-
mota_16
- Usuário Ativo

-
- Mensagens: 19
- Registrado em: Sex Dez 06, 2013 10:36
- Formação Escolar: ENSINO MÉDIO
- Área/Curso: Regular
- Andamento: cursando
 por e8group » Seg Dez 30, 2013 18:36
por e8group » Seg Dez 30, 2013 18:36
Está no caminho certo . Antes de elevar ao quadrado ,trabalhe apenas com um radical ao lado da igualdade .Logo após eleve ao quadrado e faça as simplificações e comente o que conseguiu .
-
e8group
- Colaborador Voluntário

-
- Mensagens: 1400
- Registrado em: Sex Jun 01, 2012 12:10
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica
- Andamento: cursando
 por mota_16 » Seg Dez 30, 2013 20:38
por mota_16 » Seg Dez 30, 2013 20:38
-
mota_16
- Usuário Ativo

-
- Mensagens: 19
- Registrado em: Sex Dez 06, 2013 10:36
- Formação Escolar: ENSINO MÉDIO
- Área/Curso: Regular
- Andamento: cursando
 por e8group » Seg Dez 30, 2013 21:07
por e8group » Seg Dez 30, 2013 21:07
Boa noite. Um número complexo se escreve como
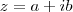
(a,b reais) e seu valor absoluto é por definição
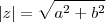
ou
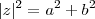
. (Há um interpretação
geométrica p/ isso,este abs pode ser encontrado via Teorema de Pitágoras ) .
Prosseguindo ...
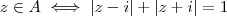
.Pondo
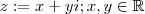
,resulta
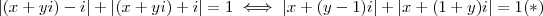
.
Seja
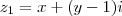
e
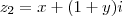
. Pelo que
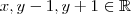
então
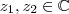
e
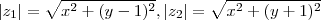
.De

, temos
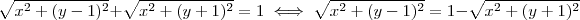
.
Agora tente concluir .
-
e8group
- Colaborador Voluntário

-
- Mensagens: 1400
- Registrado em: Sex Jun 01, 2012 12:10
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica
- Andamento: cursando
Voltar para Números Complexos
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- <=====Números Complexos-Média Geométrica=====>
por futuromilitar » Qui Mai 26, 2016 22:08
- 1 Respostas
- 9731 Exibições
- Última mensagem por DanielFerreira

Ter Mai 31, 2016 00:44
Números Complexos
-
- [Vetores]Representação Geométrica
por IlgssonBraga » Sex Jul 19, 2013 16:18
- 2 Respostas
- 2213 Exibições
- Última mensagem por IlgssonBraga

Sáb Jul 20, 2013 18:55
Geometria Analítica
-
- Representação Geométrica do quadrado da diferença
 por LuizCarlos » Qui Ago 04, 2011 02:42
por LuizCarlos » Qui Ago 04, 2011 02:42
- 3 Respostas
- 5764 Exibições
- Última mensagem por Marcelo RoX

Dom Jun 30, 2013 23:24
Álgebra Elementar
-
- [quadrado da diferença] Representação geométrica
 por LuizCarlos » Qui Ago 04, 2011 11:23
por LuizCarlos » Qui Ago 04, 2011 11:23
- 1 Respostas
- 1964 Exibições
- Última mensagem por Caradoc

Sex Ago 19, 2011 09:34
Álgebra Elementar
-
- Representação de Complexos no plano
por Jonatan » Seg Ago 02, 2010 21:54
- 1 Respostas
- 1783 Exibições
- Última mensagem por MarceloFantini

Seg Ago 09, 2010 06:05
Números Complexos
Usuários navegando neste fórum: Nenhum usuário registrado e 7 visitantes
Assunto:
[Função] do primeiro grau e quadratica
Autor:
Thassya - Sáb Out 01, 2011 16:20
1) Para que os pontos (1,3) e (-3,1) pertençam ao grafico da função f(X)=ax + b ,o valor de b-a deve ser ?
2)Qual o maior valor assumido pela função f : [-7 ,10] em R definida por f(x) = x ao quadrado - 5x + 9?
3) A função f, do primeiro grau, é definida pos f(x)= 3x + k para que o gráfico de f corte o eixo das ordenadas no ponto de ordenada 5 é?
Assunto:
[Função] do primeiro grau e quadratica
Autor:
Neperiano - Sáb Out 01, 2011 19:46
Ola
Qual as suas dúvidas?
O que você não está conseguindo fazer?
Nos mostre para podermos ajudar
Atenciosamente
Assunto:
[Função] do primeiro grau e quadratica
Autor:
joaofonseca - Sáb Out 01, 2011 20:15
1)Dados dois pontos A=(1,3) e B=(-3,1) de uma reta, é possivel definir a sua equação.


Em

substitui-se
m, substitui-se
y e
x por um dos pares ordenados, e resolve-se em ordem a
b.

2)Na equação

não existem zeros.Senão vejamos
Completando o quadrado,

As coordenadas do vertice da parabola são

O eixo de simetria é a reta

.Como se pode observar o vertice está acima do eixo Ox, estando parabola virada para cima, o vertice é um mínimo absoluto.Então basta calcular a função para os valores dos extremos do intervalo.
f(-7)=93
f(10)=59
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
![A=\left[z\in C/\left|z-i \right|+\left|z+i \right|=1 \right] A=\left[z\in C/\left|z-i \right|+\left|z+i \right|=1 \right]](/latexrender/pictures/b900fa797329be59a938e05fa7fad417.png) deve ser descrito geometricamente como:
deve ser descrito geometricamente como:
![A=\left[z\in C/\left|z-i \right|+\left|z+i \right|=1 \right] A=\left[z\in C/\left|z-i \right|+\left|z+i \right|=1 \right]](/latexrender/pictures/b900fa797329be59a938e05fa7fad417.png) deve ser descrito geometricamente como:
deve ser descrito geometricamente como:
 se exprimir por
se exprimir por 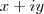 (x,y sobre
(x,y sobre  ) . Agora suponha que
) . Agora suponha que 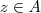 ,então a propriedade
,então a propriedade 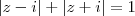 é verdadeira e substituindo z por
é verdadeira e substituindo z por 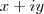 ,obterá a soma de módulos de dois números complexos . Lembre-se
,obterá a soma de módulos de dois números complexos . Lembre-se 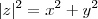 .
.
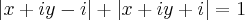
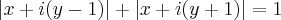
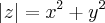 . Pensei em elevar ambos os membros ao quadrado, mas encontrei resultados que não me ajudaram. É isso? Esse é o caminho?
. Pensei em elevar ambos os membros ao quadrado, mas encontrei resultados que não me ajudaram. É isso? Esse é o caminho?

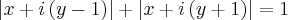
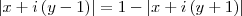
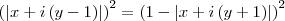
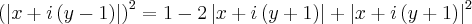
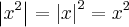
![\left[x+i\left(y-1 \right) \right]^2=1-2\left|x+i\left(y+1 \right) \right|+\left[x+i\left(y+1 \right) \right]^2 \left[x+i\left(y-1 \right) \right]^2=1-2\left|x+i\left(y+1 \right) \right|+\left[x+i\left(y+1 \right) \right]^2](/latexrender/pictures/a907049b548c337d4505897183f29556.png)

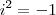
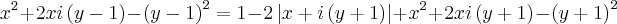
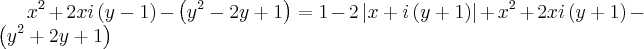
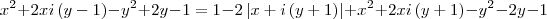


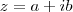 (a,b reais) e seu valor absoluto é por definição
(a,b reais) e seu valor absoluto é por definição 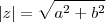 ou
ou 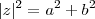 . (Há um interpretação geométrica p/ isso,este abs pode ser encontrado via Teorema de Pitágoras ) .
. (Há um interpretação geométrica p/ isso,este abs pode ser encontrado via Teorema de Pitágoras ) . 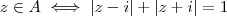 .Pondo
.Pondo 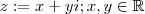 ,resulta
,resulta 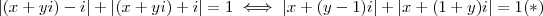 .
. 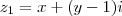 e
e 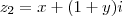 . Pelo que
. Pelo que 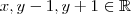 então
então 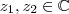 e
e 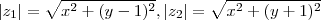 .De
.De  , temos
, temos 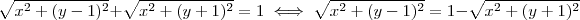 .
. 


 substitui-se m, substitui-se y e x por um dos pares ordenados, e resolve-se em ordem a b.
substitui-se m, substitui-se y e x por um dos pares ordenados, e resolve-se em ordem a b.
 não existem zeros.Senão vejamos
não existem zeros.Senão vejamos

 .Como se pode observar o vertice está acima do eixo Ox, estando parabola virada para cima, o vertice é um mínimo absoluto.Então basta calcular a função para os valores dos extremos do intervalo.
.Como se pode observar o vertice está acima do eixo Ox, estando parabola virada para cima, o vertice é um mínimo absoluto.Então basta calcular a função para os valores dos extremos do intervalo.