O subconjunto do plano complexo
![A=\left[z\in C/\left|z-i \right|+\left|z+i \right|=1 \right] A=\left[z\in C/\left|z-i \right|+\left|z+i \right|=1 \right]](/latexrender/pictures/b900fa797329be59a938e05fa7fad417.png) deve ser descrito geometricamente como:
deve ser descrito geometricamente como:a) uma circunferência
b) uma hipérbole
c) uma elipse
d) uma parábola
e) duas retas

![A=\left[z\in C/\left|z-i \right|+\left|z+i \right|=1 \right] A=\left[z\in C/\left|z-i \right|+\left|z+i \right|=1 \right]](/latexrender/pictures/b900fa797329be59a938e05fa7fad417.png) deve ser descrito geometricamente como:
deve ser descrito geometricamente como:
 se exprimir por
se exprimir por 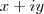 (x,y sobre
(x,y sobre  ) . Agora suponha que
) . Agora suponha que 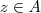 ,então a propriedade
,então a propriedade 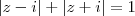 é verdadeira e substituindo z por
é verdadeira e substituindo z por 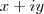 ,obterá a soma de módulos de dois números complexos . Lembre-se
,obterá a soma de módulos de dois números complexos . Lembre-se 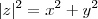 .
.
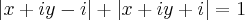
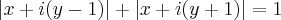
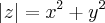 . Pensei em elevar ambos os membros ao quadrado, mas encontrei resultados que não me ajudaram. É isso? Esse é o caminho?
. Pensei em elevar ambos os membros ao quadrado, mas encontrei resultados que não me ajudaram. É isso? Esse é o caminho?

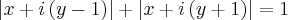
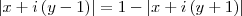
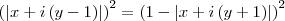
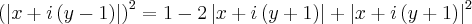
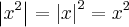
![\left[x+i\left(y-1 \right) \right]^2=1-2\left|x+i\left(y+1 \right) \right|+\left[x+i\left(y+1 \right) \right]^2 \left[x+i\left(y-1 \right) \right]^2=1-2\left|x+i\left(y+1 \right) \right|+\left[x+i\left(y+1 \right) \right]^2](/latexrender/pictures/a907049b548c337d4505897183f29556.png)

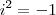
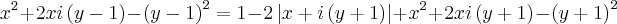
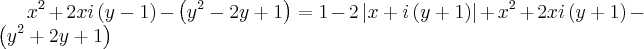
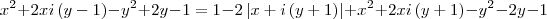


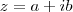 (a,b reais) e seu valor absoluto é por definição
(a,b reais) e seu valor absoluto é por definição 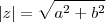 ou
ou 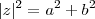 . (Há um interpretação geométrica p/ isso,este abs pode ser encontrado via Teorema de Pitágoras ) .
. (Há um interpretação geométrica p/ isso,este abs pode ser encontrado via Teorema de Pitágoras ) . 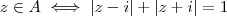 .Pondo
.Pondo 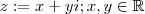 ,resulta
,resulta 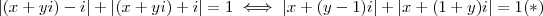 .
. 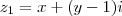 e
e 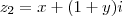 . Pelo que
. Pelo que 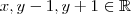 então
então 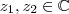 e
e 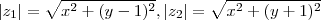 .De
.De  , temos
, temos 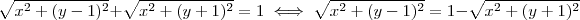 .
. 
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
![\frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}} \frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}}](/latexrender/pictures/981987c7bcdf9f8f498ca4605785636a.png)
![\sqrt[]{2} \sqrt[]{2}](/latexrender/pictures/f21662d1cabab6e8b273a4b6f1cd663a.png) (dica : igualar a expressão a
(dica : igualar a expressão a  e elevar ao quadrado os dois lados)
e elevar ao quadrado os dois lados)