A igualdade
 verifica-se para os números naturais divisíveis por qual número natural?
verifica-se para os números naturais divisíveis por qual número natural?Bom, eu sei que n = 4. Mas a questão é como eu chego em n = 4 só sabendo que
 . Sei se eu ''jogar'' n = 4 eu vou verificar a igualdade mesmo assim, mas está muito vago. Agradeço a quem puder explicar.
. Sei se eu ''jogar'' n = 4 eu vou verificar a igualdade mesmo assim, mas está muito vago. Agradeço a quem puder explicar.

 , certamente obterá algo .
, certamente obterá algo .
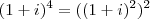 , e como
, e como 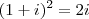 segue
segue 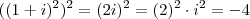 . Mesma coisa para o outro.
. Mesma coisa para o outro.

![\frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}} \frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}}](/latexrender/pictures/981987c7bcdf9f8f498ca4605785636a.png)
![\sqrt[]{2} \sqrt[]{2}](/latexrender/pictures/f21662d1cabab6e8b273a4b6f1cd663a.png)
 e elevar ao quadrado os dois lados)
e elevar ao quadrado os dois lados)