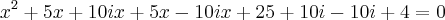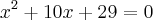Olá Estela.
A representação que você citou pode ser feita no plano de Argand-Gauss, ou plano
complexo.
No plano cartesiano, onde x e y são reais, estes números
complexos não "aparecem".
Tanto é que após, quando você encontrar a função do segundo grau pedida, represente-a no plano cartesiano e reflita sobre esta sua afirmação:
No grafico a raiz eh o ponto no eixo do x , onde y vale zero!
Você verá que como as raízes são complexas, o gráfico não toca o eixo x, diferentemente do que ocorre quando as raízes são reais.
Vou elucidar a idéia da solução.
Nesta equação:
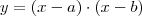
As raízes são

ou

, pois para ambos os casos teremos:
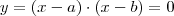
Veja, se

:
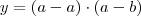
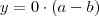

Se

:
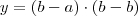


Para encontrar a equação do 2º grau pedida, substitua as raízes informadas aqui:
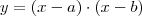
Sendo:
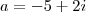
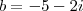
Cuidado com os sinais ao substituir.
Depois, faça a distributiva.
Também, note que a unidade imaginária é:
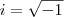
Ou seja:
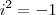
Após a distributiva, cancele algumas parcelas e substitua

por

.
Você terá a equação do 2º grau!
Por curiosidade, depois vale representar a função relacionada no gráfico para constatar que ela não toca o eixo x.
Comente caso tenha alguma dúvida.
Espero ter ajudado!





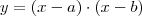
 ou
ou  , pois para ambos os casos teremos:
, pois para ambos os casos teremos: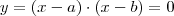
 :
: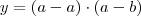
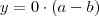

 :
: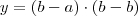


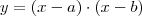
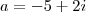
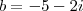
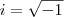
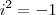
 por
por  .
.
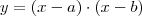 ,
,


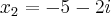
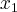 e
e  iguais a "zero" e multiplique-os.
iguais a "zero" e multiplique-os.![[x+(5-2i)][x+(5+2i)]=0 [x+(5-2i)][x+(5+2i)]=0](/latexrender/pictures/44493f5286e2a0041310dd566fa828cd.png)