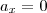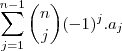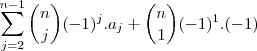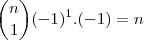-
-
Novo APOIA.se AjudaMatemática
por admin em Sáb Abr 25, 2020 19:01
- 0 Tópicos
- 478146 Mensagens
-
Última mensagem por admin

em Sáb Abr 25, 2020 19:01
-
-
Agradecimento aos Colaboradores
por admin em Qui Nov 15, 2018 00:25
- 0 Tópicos
- 531629 Mensagens
-
Última mensagem por admin

em Qui Nov 15, 2018 00:25
-
-
Ativação de Novos Registros
por admin em Qua Nov 14, 2018 11:58
- 0 Tópicos
- 495171 Mensagens
-
Última mensagem por admin

em Qua Nov 14, 2018 11:58
-
-
Regras do Fórum - Leia antes de postar!
por admin em Ter Mar 20, 2012 21:51
- 0 Tópicos
- 705151 Mensagens
-
Última mensagem por admin

em Ter Mar 20, 2012 21:51
-
-
DICA: Escrevendo Fórmulas com LaTeX via BBCode
por admin em Qua Ago 29, 2007 04:04
- 41 Tópicos
- 2120598 Mensagens
-
Última mensagem por Janayna

em Qui Abr 27, 2017 00:04
 por silvanuno11 » Sex Mai 25, 2012 12:45
por silvanuno11 » Sex Mai 25, 2012 12:45
Boa tarde,
Alguém me pode ajudar a resolver o seguinte exercício?
Obrigado
Abraço
- Anexos
-

-
silvanuno11
- Novo Usuário

-
- Mensagens: 5
- Registrado em: Seg Mar 26, 2012 20:15
- Formação Escolar: SUPLETIVO
- Andamento: cursando
 por silvanuno11 » Seg Mai 28, 2012 06:36
por silvanuno11 » Seg Mai 28, 2012 06:36
Bom dia.
Obrigado pela ajuda. Foi importante.
Abraço.
-
silvanuno11
- Novo Usuário

-
- Mensagens: 5
- Registrado em: Seg Mar 26, 2012 20:15
- Formação Escolar: SUPLETIVO
- Andamento: cursando
Voltar para Binômio de Newton
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Justificar a afirmação
 por silvanuno11 » Dom Mai 27, 2012 16:30
por silvanuno11 » Dom Mai 27, 2012 16:30
- 1 Respostas
- 1402 Exibições
- Última mensagem por PeterHiggs

Qui Mai 31, 2012 11:22
Álgebra Elementar
-
- Logaritmos.( Prove tal afirmação )
por DanielRJ » Qui Out 14, 2010 18:15
- 5 Respostas
- 3309 Exibições
- Última mensagem por MarceloFantini

Sex Out 15, 2010 18:41
Logaritmos
-
- Prove se a afirmação é verdadeira
por Well » Dom Abr 01, 2012 18:14
- 3 Respostas
- 2066 Exibições
- Última mensagem por fraol

Seg Abr 02, 2012 14:42
Álgebra Elementar
-
- [Matrizes] Comentar uma afirmação
por fff » Sex Out 10, 2014 07:56
- 0 Respostas
- 2185 Exibições
- Última mensagem por fff

Sex Out 10, 2014 07:56
Matrizes e Determinantes
-
- [Matrizes] Verificação de afirmação e prova
por Andre Arruda » Ter Mar 25, 2014 16:55
- 2 Respostas
- 3121 Exibições
- Última mensagem por Andre Arruda

Qui Mar 27, 2014 17:28
Matrizes e Determinantes
Usuários navegando neste fórum: Nenhum usuário registrado e 5 visitantes
Assunto:
Funções
Autor:
Emilia - Sex Dez 03, 2010 13:24
Preciso de ajuda no seguinte problema:
O governo de um Estado Brasileiro mudou a contribuição previdenciária de seus contribuintes. era de 6% sobre qualquer salário; passou para 11% sobre o que excede R$1.200,00 nos salários. Por exemplo, sobre uma salário de R$1.700,00, a contribuição anterior era: 0,06x R$1.700,00 = R$102,00; e a atual é: 0,11x(R$1.700,00 - R$1.200,00) = R$55,00.
i. Determine as funções que fornecem o valor das contribuições em função do valor x do salário antes e depois da mudança na forma de cobrança.
ii. Esboce seus gráficos.
iii. Determine os valores de salários para os quais:
- a contribuição diminuiu;
- a contribuição permaneceu a mesma;
- a contribuição aumentou.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.



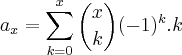
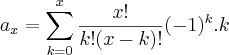
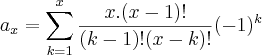
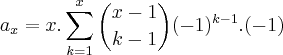
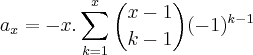
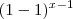 :
: