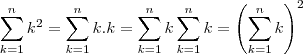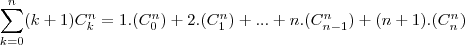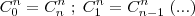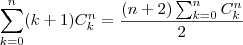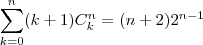por Douglasm » Ter Fev 23, 2010 11:17
por Douglasm » Ter Fev 23, 2010 11:17
Eu resolvi a seguinte questão e encontrei uma resposta diferente do gabarito. Eis a questão:
Calcule
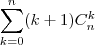
.
Minha resolução:
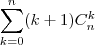
=
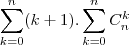
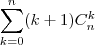
=
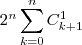
(Os resultados são obtidos através dos teoremas das colunas e das linhas do triângulo de Pascal, respectivamente.)
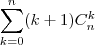
=
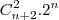
=
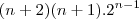
No gabarito a resposta é somente
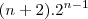
Será que estou fazendo errado mesmo ou o gabarito esqueceu o (n+1)?
-

Douglasm
- Colaborador Voluntário

-
- Mensagens: 270
- Registrado em: Seg Fev 15, 2010 10:02
- Formação Escolar: ENSINO MÉDIO
- Andamento: formado
 por Mathmatematica » Dom Jun 06, 2010 21:44
por Mathmatematica » Dom Jun 06, 2010 21:44
Olá Douglas!
Infelizmente você está fazendo errado. A passagem
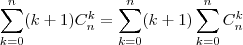
está errada. Não entendi muito bem o que é
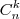
(não seria
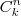
?).
Mas voltando ao erro: o fator

possui um

e o

no somatório está variando. Da mesma forma, o fator
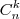
também possui um

e, no somatório, o

varia. Como o que eu sei sobre somatório é pouco vou tentar explicar com um contra-exemplo para aquela passagem:
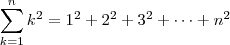
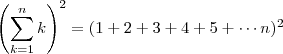
Como podemos perceber
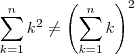
. De acordo com a sua passagem teríamos:
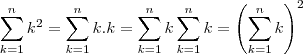
Espero que tenha entendido. (Vou estudar mais o assunto.... Preciso explicar melhor!!!)
-
Mathmatematica
- Usuário Dedicado

-
- Mensagens: 25
- Registrado em: Sex Jun 04, 2010 23:53
- Formação Escolar: ENSINO MÉDIO
- Área/Curso: Bacharelado
- Andamento: cursando
Voltar para Binômio de Newton
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
[calculo] derivada
Autor:
beel - Seg Out 24, 2011 16:59
Para derivar a função
(16-2x)(21-x).x
como é melhor fazer?
derivar primeiro sei la, ((16-2x)(21-x))' achar o resultado (y)
e depois achar (y.x)' ?
Assunto:
[calculo] derivada
Autor:
MarceloFantini - Seg Out 24, 2011 17:15
Você poderia fazer a distributiva e derivar como um polinômio comum.
Assunto:
[calculo] derivada
Autor:
wellersonobelix - Dom Mai 31, 2015 17:26
Funciona da mesma forma que derivada de x.y.z, ou seja, x'.y.z+x.y'.z+x.y.z' substitui cada expressão pelas variáveis e x',y' e z' é derivada de cada um
Assunto:
[calculo] derivada
Autor:
wellersonobelix - Dom Mai 31, 2015 17:31
derivada de (16-2x)=-2
derivada de (21-x)=-1
derivada de x=1
derivada de (16-2x)(21-x)x=-2.(21-x)x+(-1).(16-2x)x +1.(16-2x)(21-x)
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
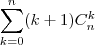 .
.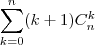 =
= 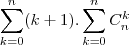
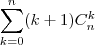 =
= 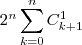
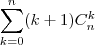 =
= 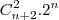 =
= 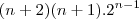
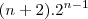


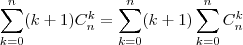 está errada. Não entendi muito bem o que é
está errada. Não entendi muito bem o que é 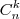 (não seria
(não seria 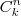 ?).
?). possui um
possui um  e o
e o 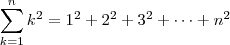
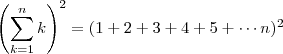
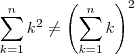 . De acordo com a sua passagem teríamos:
. De acordo com a sua passagem teríamos: