-
-
Novo APOIA.se AjudaMatemática
por admin em Sáb Abr 25, 2020 19:01
- 0 Tópicos
- 477725 Mensagens
-
Última mensagem por admin

em Sáb Abr 25, 2020 19:01
-
-
Agradecimento aos Colaboradores
por admin em Qui Nov 15, 2018 00:25
- 0 Tópicos
- 528578 Mensagens
-
Última mensagem por admin

em Qui Nov 15, 2018 00:25
-
-
Ativação de Novos Registros
por admin em Qua Nov 14, 2018 11:58
- 0 Tópicos
- 492145 Mensagens
-
Última mensagem por admin

em Qua Nov 14, 2018 11:58
-
-
Regras do Fórum - Leia antes de postar!
por admin em Ter Mar 20, 2012 21:51
- 0 Tópicos
- 696483 Mensagens
-
Última mensagem por admin

em Ter Mar 20, 2012 21:51
-
-
DICA: Escrevendo Fórmulas com LaTeX via BBCode
por admin em Qua Ago 29, 2007 04:04
- 41 Tópicos
- 2105128 Mensagens
-
Última mensagem por Janayna

em Qui Abr 27, 2017 00:04
 por EREGON » Ter Abr 14, 2015 06:29
por EREGON » Ter Abr 14, 2015 06:29
Bom dia,
estou com dificuldades em efectuar esta prova sem recorrer à IM, no entanto tendo como suporte as matérias já dadas, como:
1 - Funções Injetivas, sobrejetivas e bijeticvas.
2 - Cardinalidades.
3 - Coeficientes binomiais.
4 - Permutações e combinações.
5 - Binomio de Newton, triangulo de pascal, lei de simetria, etc.
Tentei fazer este desenvolvimento que não sei se está correto, mas depois não consegui avançar mais

:
- Anexos
-
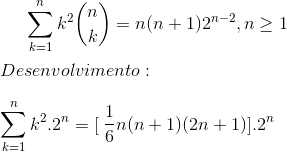
- CodeCogsEqn.gif (3.02 KiB) Exibido 3423 vezes
-
EREGON
- Usuário Ativo

-
- Mensagens: 12
- Registrado em: Seg Nov 10, 2014 16:00
- Formação Escolar: ENSINO MÉDIO
- Área/Curso: informatica
- Andamento: cursando
 por EREGON » Qui Abr 16, 2015 14:07
por EREGON » Qui Abr 16, 2015 14:07
Olá boa tarde,
alguém me poderá auxiliar neste exercício?
Obrigado.
-
EREGON
- Usuário Ativo

-
- Mensagens: 12
- Registrado em: Seg Nov 10, 2014 16:00
- Formação Escolar: ENSINO MÉDIO
- Área/Curso: informatica
- Andamento: cursando
 por e8group » Sex Abr 17, 2015 23:12
por e8group » Sex Abr 17, 2015 23:12
Podemos generalizar , computar
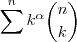
recursivamente em função das somas
![]\sum^n k^\zeta \binom{n}{k} ; 0 \leq \zeta < \alpha ]\sum^n k^\zeta \binom{n}{k} ; 0 \leq \zeta < \alpha](/latexrender/pictures/f0bb1785e500fb558475b101925ad1bf.png)
.
Defina , para
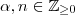
,

.
Veja que
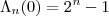
(verifique ) . Fixe
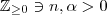
arbitrariamente .
Para cada
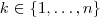
, veja que

.
Pondo ,
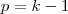
, temos
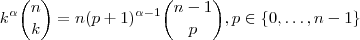
.
Como ,
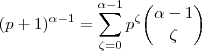
, substituindo na expressão acima , temos
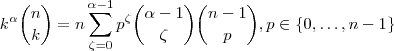
. Finalmente , substituindo esta expressão na soma , vem
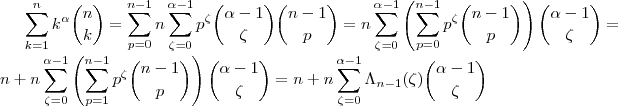
, ou seja
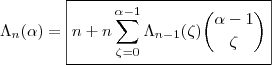
.
Agora somos capazes facilmente , de computar por exemplo
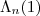
. De acordo com a formula acima ,
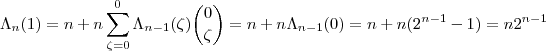
.
o exercício é um corolário do resultado acima ... Segue-se então que
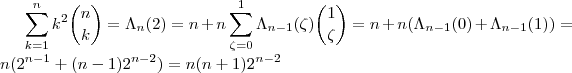
.
-
e8group
- Colaborador Voluntário

-
- Mensagens: 1400
- Registrado em: Sex Jun 01, 2012 12:10
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica
- Andamento: cursando
Voltar para Binômio de Newton
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [Somatório] Provar pelo Método de Indução Matemática
por Prof Prevaricador » Dom Abr 14, 2013 16:25
- 2 Respostas
- 4736 Exibições
- Última mensagem por Prof Prevaricador

Dom Abr 14, 2013 18:35
Sequências
-
- Provar por indução
por Cleyson007 » Sex Abr 13, 2012 15:27
- 3 Respostas
- 1857 Exibições
- Última mensagem por Cleyson007

Sex Abr 13, 2012 16:17
Álgebra Elementar
-
- Duvida em provar por Indução
por carlosecc » Sáb Dez 08, 2012 21:53
- 3 Respostas
- 1777 Exibições
- Última mensagem por carlosecc

Dom Dez 09, 2012 20:39
Teoria dos Números
-
- [hipótese da indução] Indução matemática
por leonardoandra » Sáb Out 12, 2013 22:58
- 1 Respostas
- 2241 Exibições
- Última mensagem por leonardoandra

Seg Out 14, 2013 20:10
Equações
-
- Indução Matemática
por gramata » Qua Set 02, 2009 16:52
- 0 Respostas
- 2716 Exibições
- Última mensagem por gramata

Qua Set 02, 2009 16:52
Problemas do Cotidiano
Usuários navegando neste fórum: Nenhum usuário registrado e 2 visitantes
Assunto:
(FGV) ... função novamente rs
Autor:
my2009 - Qua Dez 08, 2010 21:48
Uma função polinomial f do 1° grau é tal que f(3) = 6 e f(4) = 8.Portanto o valor de f(10) é :
Assunto:
(FGV) ... função novamente rs
Autor: Anonymous - Qui Dez 09, 2010 17:25
Uma função de 1º grau é dada por

.
Temos que para

,

e para

,

.

Ache o valor de

e

, monte a função e substitua

por

.
Assunto:
(FGV) ... função novamente rs
Autor:
Pinho - Qui Dez 16, 2010 13:57
my2009 escreveu:Uma função polinomial f do 1° grau é tal que f(3) = 6 e f(4) = 8.Portanto o valor de f(10) é :
f(x)= 2.x
f(3)=2.3=6
f(4)=2.4=8
f(10)=2.10=20
Assunto:
(FGV) ... função novamente rs
Autor:
dagoth - Sex Dez 17, 2010 11:55
isso ai foi uma questao da FGV?
haahua to precisando trocar de faculdade.
Assunto:
(FGV) ... função novamente rs
Autor:
Thiago 86 - Qua Mar 06, 2013 23:11
Saudações!

ví suaquestão e tentei resolver, depois você conta-me se eu acertei.
Uma função de 1º grau é dada por y=3a+b
Resposta :
3a+b=6 x(4)
4a+b=8 x(-3)
12a+4b=24
-12a-3b=-24
b=0
substituindo b na 1°, ttenho que: 3a+b=6
3a+0=6
a=2
substituindo em: y=3a+b
y=30+0
y=30

Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
 :
:

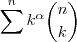 recursivamente em função das somas
recursivamente em função das somas ![]\sum^n k^\zeta \binom{n}{k} ; 0 \leq \zeta < \alpha ]\sum^n k^\zeta \binom{n}{k} ; 0 \leq \zeta < \alpha](/latexrender/pictures/f0bb1785e500fb558475b101925ad1bf.png) .
. 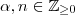 ,
,  .
. 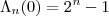 (verifique ) . Fixe
(verifique ) . Fixe 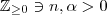 arbitrariamente .
arbitrariamente .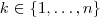 , veja que
, veja que  .
. 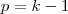 , temos
, temos 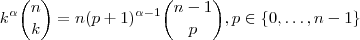 .
. 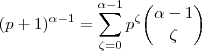 , substituindo na expressão acima , temos
, substituindo na expressão acima , temos 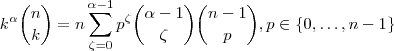 . Finalmente , substituindo esta expressão na soma , vem
. Finalmente , substituindo esta expressão na soma , vem 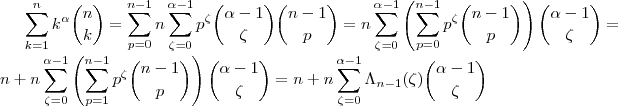 , ou seja
, ou seja 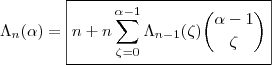 .
.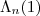 . De acordo com a formula acima ,
. De acordo com a formula acima , 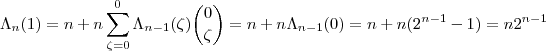 .
. 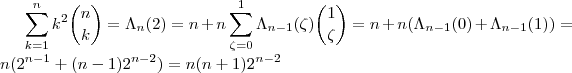 .
.
 .
. ,
,  e para
e para  ,
,  .
.
 e
e  , monte a função e substitua
, monte a função e substitua  por
por  .
.
