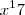 no desenvolvimento de
no desenvolvimento de 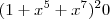

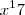 no desenvolvimento de
no desenvolvimento de 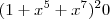

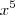 em evidencia , teremos
em evidencia , teremos ![(1 + x^5 +x^7)^{20} = (1 +[x^5(1 +x^2)])^20 (1 + x^5 +x^7)^{20} = (1 +[x^5(1 +x^2)])^20](/latexrender/pictures/0ad7338f8254c716abb315c1a063622d.png) .Pelo teorema binomial ,
.Pelo teorema binomial ,![1 +[x^5(1 +x^2)])^20= \sum_{k=0}^{20} \binom{20}{k} [x^5(1+x^2)]^k = \sum_{k=0}^{20} \binom{20}{k} x^{5k}(1+x^2)^k = 1 + \binom{20}{1}x^5(1+x^2 ) + \binom{20}{2}x^{10}(1+x^2)^2 + \binom{20}{3}x^{15}(1 +x^2)^3 + \sum_{k=4}^{20} \binom{20}{k} [x^5(1+x^2)]^k 1 +[x^5(1 +x^2)])^20= \sum_{k=0}^{20} \binom{20}{k} [x^5(1+x^2)]^k = \sum_{k=0}^{20} \binom{20}{k} x^{5k}(1+x^2)^k = 1 + \binom{20}{1}x^5(1+x^2 ) + \binom{20}{2}x^{10}(1+x^2)^2 + \binom{20}{3}x^{15}(1 +x^2)^3 + \sum_{k=4}^{20} \binom{20}{k} [x^5(1+x^2)]^k](/latexrender/pictures/6b190677aa82f28ec474211533c54f62.png) .
.  é oriundo da 4 parcela
é oriundo da 4 parcela 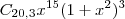 . Basta desenvolver para encontrar o coefc.
. Basta desenvolver para encontrar o coefc. 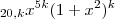 , o grau de x será sempre menor que
, o grau de x será sempre menor que 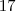 quando
quando 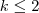 (afinal de contas
(afinal de contas 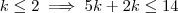 ) e maior que
) e maior que 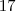 quando
quando 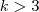 (afinal de contas
(afinal de contas 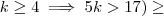 ) .
) .



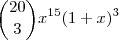 e
e 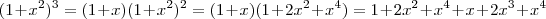 . O único termo que nos interessa é
. O único termo que nos interessa é 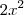 , pois
, pois 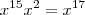 . Então o coefc. é
. Então o coefc. é 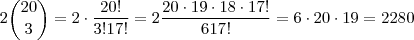 .
.

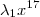 vem da expressão
vem da expressão 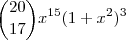 . Ao desenvolvermos
. Ao desenvolvermos 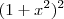 precisaremos de
precisaremos de 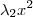 . Pois , produto de números de mesma base conserva a base e soma os expoentes . Logo o coef. será
. Pois , produto de números de mesma base conserva a base e soma os expoentes . Logo o coef. será 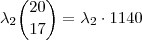 . Agora vamos determinar
. Agora vamos determinar 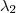 .
. 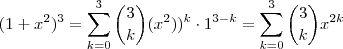 . Precisamos apenas de
. Precisamos apenas de 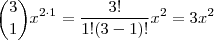 . Assim , o nosso
. Assim , o nosso 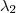 é 3 , logo a resposta será
é 3 , logo a resposta será 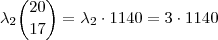 . Por favor , agora check a resposta .
. Por favor , agora check a resposta .


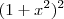 " na resposta os termos dentro doparenteses é elevado a 2 ou 3.
" na resposta os termos dentro doparenteses é elevado a 2 ou 3.
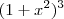 ... . As potências de (x^2) serão sempre 0,1,2,3 . Todos naturais menores que 3 , Ou ainda , As potências de x serão 0,2,4,6 .
... . As potências de (x^2) serão sempre 0,1,2,3 . Todos naturais menores que 3 , Ou ainda , As potências de x serão 0,2,4,6 . 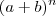 cada parcela será da forma
cada parcela será da forma 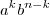 com
com 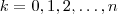 . Portanto , as potências de
. Portanto , as potências de 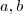 são naturais variando de zero até n .
são naturais variando de zero até n .

Usuários navegando neste fórum: Nenhum usuário registrado e 4 visitantes
![\frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}} \frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}}](/latexrender/pictures/981987c7bcdf9f8f498ca4605785636a.png)
![\sqrt[]{2} \sqrt[]{2}](/latexrender/pictures/f21662d1cabab6e8b273a4b6f1cd663a.png) (dica : igualar a expressão a
(dica : igualar a expressão a  e elevar ao quadrado os dois lados)
e elevar ao quadrado os dois lados)