 por cristina » Sex Ago 20, 2010 23:47
por cristina » Sex Ago 20, 2010 23:47
Boa noite estou precisando de ajuda
O termo independente de x no desenvolvimento de
![\left(\frac{1}{{x}^{2}} -\sqrt[4]{x} \right){}^{18} \left(\frac{1}{{x}^{2}} -\sqrt[4]{x} \right){}^{18}](/latexrender/pictures/2c9ca24bbae681ad7c9da8ecfbba77c7.png)
é:
se alguem puder me ajudar agradeço
-
cristina
- Usuário Parceiro

-
- Mensagens: 82
- Registrado em: Qua Set 02, 2009 17:49
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura/ matematica
- Andamento: cursando
 por VtinxD » Dom Ago 22, 2010 01:50
por VtinxD » Dom Ago 22, 2010 01:50
Para achar o termo independente desta função binomial a forma que conheço seria usar o termo geral de um binomio.Onde o termo independente é aquele onde o x tem coeficiente igual a zero.
![f(x)={\left(1/{x}^{2} - \sqrt[4]{x} \right)}^{18} f(x)={\left(1/{x}^{2} - \sqrt[4]{x} \right)}^{18}](/latexrender/pictures/555f1620520737bf8dd4b8e1237332b9.png)
Onde T é o termo geral da função f(x):
![{T}_{n+1}= \frac{18!}{n!\left(18-n \right)!}. \left({1/{x}^{2}} \right)^{18-n} .\left({-\sqrt[4]{x}} \right)^{n} {T}_{n+1}= \frac{18!}{n!\left(18-n \right)!}. \left({1/{x}^{2}} \right)^{18-n} .\left({-\sqrt[4]{x}} \right)^{n}](/latexrender/pictures/e6095ef015bd8dfcf5b6c11e198db2f2.png)
Para achar o termo indepente,primeiro temos que achar qual termo ,logo o valor de n :
![\left({1/{x}^{2}} \right)^{18-n}. \left({-\sqrt[4]{x}} \right)^{n} = {x}^{0} \left({1/{x}^{2}} \right)^{18-n}. \left({-\sqrt[4]{x}} \right)^{n} = {x}^{0}](/latexrender/pictures/bbe16b7c9c701b9554e816eab8ce0f2a.png)
Colocando de uma forma mais amigavel:
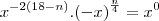
Na multiplicação se soma os espoentes e nesse caso os iguala a zero para que igualdade se torne valida.
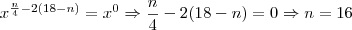
Substituindo na formula do termo geral:
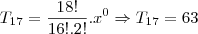
`
É o meu primeiro post e foi bem complicado trabalhar com o editor de formulas, espero ter ajudado e tambem que esteja certo

.
-
VtinxD
- Usuário Parceiro

-
- Mensagens: 64
- Registrado em: Dom Ago 15, 2010 18:29
- Formação Escolar: ENSINO MÉDIO
- Área/Curso: Bacharelado em Matematica
- Andamento: cursando
 por cristina » Dom Ago 22, 2010 10:48
por cristina » Dom Ago 22, 2010 10:48
Obrigada pela a ajuda
Não tenho a resposta, pois é aberto, mas depois te digo se esta certo.
-
cristina
- Usuário Parceiro

-
- Mensagens: 82
- Registrado em: Qua Set 02, 2009 17:49
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura/ matematica
- Andamento: cursando
Voltar para Binômio de Newton
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- TERMO INDEPENDENTE DE X
por hudeslan » Seg Ago 17, 2009 19:28
- 2 Respostas
- 22089 Exibições
- Última mensagem por Molina

Seg Ago 17, 2009 23:18
Estatística
-
- Probabilidade independente
por bianca12 » Qua Out 30, 2013 22:06
- 0 Respostas
- 1375 Exibições
- Última mensagem por bianca12

Qua Out 30, 2013 22:06
Probabilidade
-
- acerto independente
por dandara » Dom Abr 24, 2016 11:28
- 0 Respostas
- 4865 Exibições
- Última mensagem por dandara

Dom Abr 24, 2016 11:28
Probabilidade
-
- Determinar se é linearmente independente
por Razoli » Dom Set 14, 2014 20:36
- 1 Respostas
- 1910 Exibições
- Última mensagem por e8group

Seg Set 15, 2014 09:47
Álgebra Linear
-
- Probabilidade Condicionada/ Acontecimento Independente
por Mcatia » Qua Nov 10, 2010 16:25
- 5 Respostas
- 4400 Exibições
- Última mensagem por fraol

Ter Abr 17, 2012 22:18
Probabilidade
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
(FGV) ... função novamente rs
Autor:
my2009 - Qua Dez 08, 2010 21:48
Uma função polinomial f do 1° grau é tal que f(3) = 6 e f(4) = 8.Portanto o valor de f(10) é :
Assunto:
(FGV) ... função novamente rs
Autor: Anonymous - Qui Dez 09, 2010 17:25
Uma função de 1º grau é dada por

.
Temos que para

,

e para

,

.

Ache o valor de

e

, monte a função e substitua

por

.
Assunto:
(FGV) ... função novamente rs
Autor:
Pinho - Qui Dez 16, 2010 13:57
my2009 escreveu:Uma função polinomial f do 1° grau é tal que f(3) = 6 e f(4) = 8.Portanto o valor de f(10) é :
f(x)= 2.x
f(3)=2.3=6
f(4)=2.4=8
f(10)=2.10=20
Assunto:
(FGV) ... função novamente rs
Autor:
dagoth - Sex Dez 17, 2010 11:55
isso ai foi uma questao da FGV?
haahua to precisando trocar de faculdade.
Assunto:
(FGV) ... função novamente rs
Autor:
Thiago 86 - Qua Mar 06, 2013 23:11
Saudações!

ví suaquestão e tentei resolver, depois você conta-me se eu acertei.
Uma função de 1º grau é dada por y=3a+b
Resposta :
3a+b=6 x(4)
4a+b=8 x(-3)
12a+4b=24
-12a-3b=-24
b=0
substituindo b na 1°, ttenho que: 3a+b=6
3a+0=6
a=2
substituindo em: y=3a+b
y=30+0
y=30

Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
![\left(\frac{1}{{x}^{2}} -\sqrt[4]{x} \right){}^{18} \left(\frac{1}{{x}^{2}} -\sqrt[4]{x} \right){}^{18}](/latexrender/pictures/2c9ca24bbae681ad7c9da8ecfbba77c7.png) é:
é:
![\left(\frac{1}{{x}^{2}} -\sqrt[4]{x} \right){}^{18} \left(\frac{1}{{x}^{2}} -\sqrt[4]{x} \right){}^{18}](/latexrender/pictures/2c9ca24bbae681ad7c9da8ecfbba77c7.png) é:
é:
![f(x)={\left(1/{x}^{2} - \sqrt[4]{x} \right)}^{18} f(x)={\left(1/{x}^{2} - \sqrt[4]{x} \right)}^{18}](/latexrender/pictures/555f1620520737bf8dd4b8e1237332b9.png)
![{T}_{n+1}= \frac{18!}{n!\left(18-n \right)!}. \left({1/{x}^{2}} \right)^{18-n} .\left({-\sqrt[4]{x}} \right)^{n} {T}_{n+1}= \frac{18!}{n!\left(18-n \right)!}. \left({1/{x}^{2}} \right)^{18-n} .\left({-\sqrt[4]{x}} \right)^{n}](/latexrender/pictures/e6095ef015bd8dfcf5b6c11e198db2f2.png)
![\left({1/{x}^{2}} \right)^{18-n}. \left({-\sqrt[4]{x}} \right)^{n} = {x}^{0} \left({1/{x}^{2}} \right)^{18-n}. \left({-\sqrt[4]{x}} \right)^{n} = {x}^{0}](/latexrender/pictures/bbe16b7c9c701b9554e816eab8ce0f2a.png)
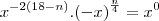
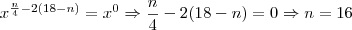
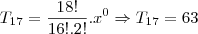 `
`

 .
. ,
,  e para
e para  ,
,  .
.
 e
e  , monte a função e substitua
, monte a função e substitua  por
por  .
.
